Obliczenia – optymalna średnica rurociągu

Metody wyznaczania krzywej kosztów inwestycyjnych

Metody wyznaczania jednostkowego kosztu eksploatacyjnych

  1. Na podstawie znanego kosztu jednej inwestycji

Jeżeli znamy parametry i koszty wybudowanego rurociągu to możemy te informacje wykorzystać do wyznaczania krzywej kosztów inwestycyjnych.

    • L = 1500 m –  długość rurociągu
    • H = 15 m –  geometryczna wysokość podnoszenia
    • PE 100 DN160 PN16 –  ryp rury
    • Ki = 600000 zł – koszt inwestycyjny

Krok 1. Koszty zmienne

Na podstawie danych cennikowych: rur, robocizny, maszyn itp. dzielimy koszty na stałe i zmienne. W omawianym przykładzie podzieliliśmy koszty 50% / 50%.

    • Ks = 300000 zł – stały koszt inwestycyjny (np. administracja, projekt, nadzór)
    • Kz = 300000 zł – zmienny koszt inwestycyjny (np. materiały, montaż, robocizna)

Krok 2. Średnica odniesienia

Na podstawie danych katalogowych obliczamy średnicę odniesienia do (wewnętrzną średnicę rurociągu).

d_o = d_z - 2 \cdot e = 160 - 2 \cdot 14,7 = 131 mm   (1)

Krok 3. Koszt odniesienia

Z analizy wzoru Optymalna średnica rurociągu (20) wiemy, że koszty stałe ks nie mają wpływy na średnicę optymalną. Na podstawie kosztu zmiennego Kz i długości rurociągu L obliczamy koszt odniesienia ko (koszt 1 m rurociągu).

k_o = {K_z \over L} = {300000 \over 1500} = 200 zł/m   (2)

Krok 4. Krzywa kosztów inwestycyjnych

Krzywą kosztów inwestycyjnych wyznaczamy na podstawie wzoru (3).

k_i = {k_o \over d_o^2} \cdot d = {200 \over 0,131^2} \cdot d    (3)

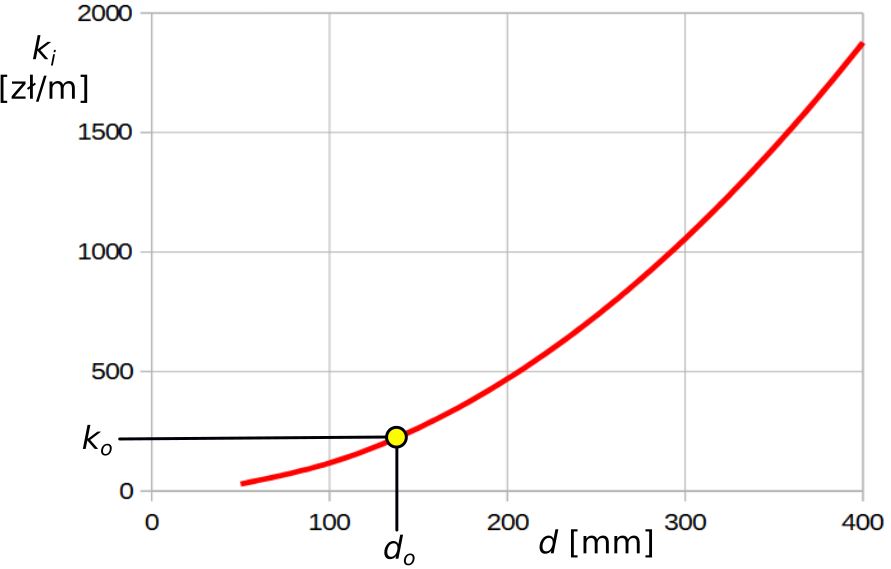
Rys.1. Jednostkowe koszty inwestycyjne w zależności od średnicy rurociągu

2. Na podstawie znanego kosztu dwóch inwestycji

Jeżeli znamy parametry i koszty dwóch wybudowanych rurociągów to możemy te informacje wykorzystać do wyznaczania jednostkowych kosztów stałych ks i krzywej jednostkowych kosztów zmiennych kz.

    • L1 = 1500 m
    • PE 100 DN160 PN16
    • K1 = 600000 zł
    • L2 = 2500 m
    • PE 100 DN250 PN16 –  typ rury
    • K2 = 1800000 zł – koszt inwestycyjny

Krok 1. Całkowite koszty jednostkowe inwestycji

Całkowite koszty jednostkowe inwestycji 1 i 2 obliczamy ze wzorów (4) i (5).

k_1 = {K_1 \over L_1} = {600000 \over 1500} = 400 zł/m   (4)

k_2 = {K_2 \over L_2} = {1800000 \over 2500} = 720 zł/m   (5)

Krok 2. Średnica odniesienia

Średnicę wewnętrzną rurociągów obliczamy ze wzorów (6) i (7).

d_1 = d_z - 2 \cdot e = 160 - 2 \cdot 14,7 = 131 mm   (6)

d_2 = d_z - 2 \cdot e = 250 - 2 \cdot 22,7 = 205 mm   (7)

Krok 3. Współczynnik kosztów zmiennych

Na podstawie równań Optymalna średnica rurociągu (6) i (7) możemy napisać ogólne równanie na koszt jednostkowe inwestycji w postaci (8) i (9).

k_1 = k_s + A \cdot d_1^2   (8)

k_2 = k_s + A \cdot d_2^2   (9)

Po odjęciu stronami równania (8) od (9) otrzymamy równanie opisujące współczynnik kosztów zmiennych (10).

A = {k_2 - k_1 \over d_2^2 -  d_1^2} =  {720 - 400 \over 205^2-131^2} = 0,0129   (10)

Krok 4. Jednostkowy koszt stały

Po podstawieniu wartości do równania (8) wyznaczamy jednostkowy koszt stały z równania (11).

k_s = k_1 - A \cdot d_1^2 = 400 - 0,0129 \cdot 131^2 = 180 zł/m  (11)

Krok 5. Krzywa kosztów inwestycyjnych

Na podstawie wzoru (8), wyznaczamy krzywą kosztów zmiennych (12) i całkowitych (13)

k_z =  A \cdot d^2 zł/m  (12)

k = k_s + A \cdot d^2 zł/m  (13)

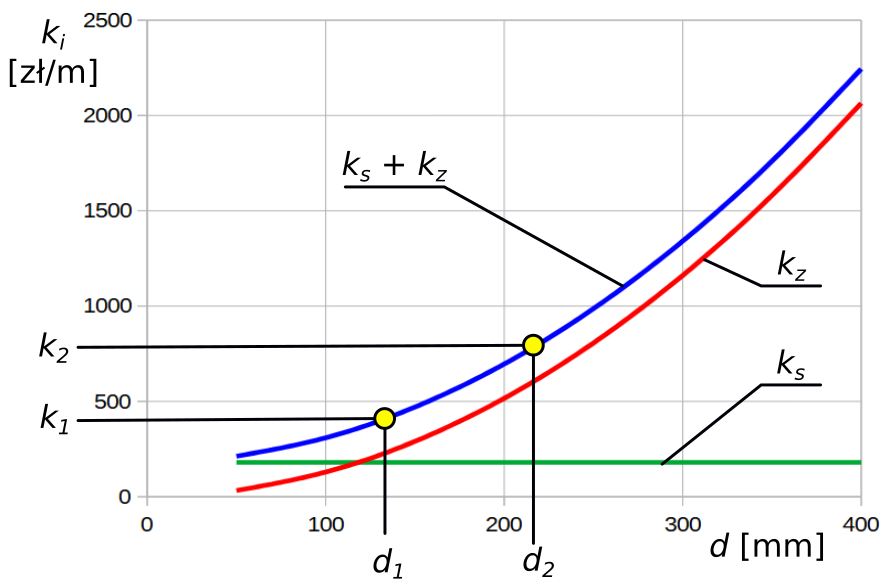
Rys.2. Jednostkowe koszty stałe i zmienne w zależności od średnicy rurociągu

3. Na podstawie znanych kosztów trzech (lub więcej) inwestycji

Jeżeli znamy parametry i koszty wielu wybudowanych rurociągów to możemy te informacje wykorzystać do wyznaczania funkcji kosztów inwestycyjnych na podstawie krzywej regresji.

    • L1 = 1500 m
    • PE 100 DN160 PN16
    • K1 = 600000 zł
    • L2 = 2500 m
    • PE 100 DN250 PN16 –  typ rury
    • K2 = 1800000 zł – koszt inwestycyjny
    • L3 = 1000 m
    • PE 100 DN315 PN16 –  typ rury
    • K3 = 1800000 zł – koszt inwestycyjny

Krok 1. Całkowite koszty jednostkowe inwestycji

k_1 = {K_1 \over L_1} = {600000 \over 1500} = 400 zł/m   (14)

k_2 = {K_2 \over L_2} = {1800000 \over 2500} = 720 zł/m   (15)

k_3 = {K_3 \over L_3} = {1040000 \over 1000} = 1040 zł/m   (16)

Krok 2. Średnica odniesienia

d_1 = d_z - 2 \cdot e = 160 - 2 \cdot 14,7 = 131 mm   (17)

d_2 = d_z - 2 \cdot e = 250 - 2 \cdot 22,7 = 205 mm   (18)

d_3 = d_z - 2 \cdot e = 315 - 2 \cdot 28,6 = 205 mm   (18)

Krok 3. Regresja krzywej kosztów

Wprowadzamy dane z kroku 1 i 2 do dowolnego arkusza kalkulacyjnego LibreOffice Calc, Excell, jak to pokazano na rys. 3. Arkusze te mają wbudowane procedury obliczania różnych funkcji regresji metodą najmniejszych kwadratów.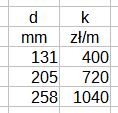

Rys. 3. Dane o inwestycjach wprowadzone do arkusza kalkulacyjnego

Z rozważań na stronie Optymalna średnica rurociągu (5) wynika, że z wystarczającą dokładnością funkcja kosztów inwestycyjnych może być przybliżona krzywą kwadratową. Dokładność aproksymacji będzie tym większa im dane źródłowe (średnice) będą bliższe wartości obliczonej średnicy optymalnej.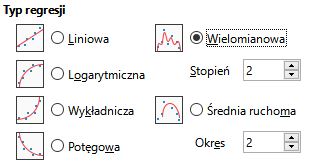

Rys. 4. Ustawienia typu funkcji regresji

Do wyznaczania średnicy optymalnej mogą być wykorzystywane zarówno funkcje opisujące koszty zmienne, jak i całkowite jednostkowe koszty inwestycyjne. Koszty stałe ks nie mają wpływu na wynik obliczeń.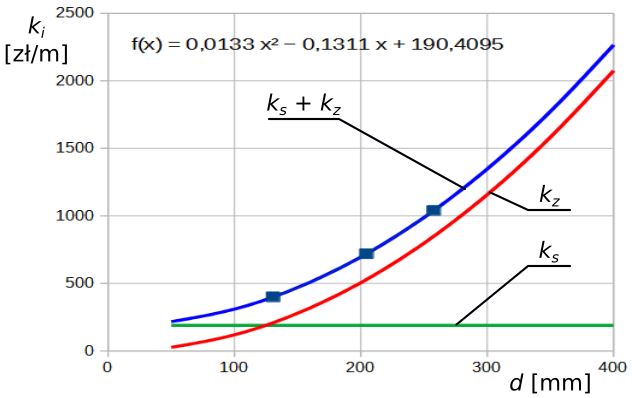

Rys. 5. Jednostkowe koszty stałe i zmienne wyznaczone na podstawie funkcji regresji

4. Jednostkowy koszt eksploatacji, bez zmiany wartości pieniądza

W przykładzie uwzględniono jedynie koszty energii, w rzeczywistości koszty eksploatacji mogą zawierać inne składniki.

Planowane parametry pracy rurociągu

    • Q = 150 m3/h – przepływ
    • kj = 1 zł/kWh – koszt jednostkowy energii

W tym przypadku, średnicę optymalną można wyznaczyć bezpośrednio na podstawie wzoru Optymalna średnica rurociągu (20). Jednostkowe koszty energii (na 1 m długości rurociągu w ciągu 1 s) na podstawie Optymalna średnica rurociągu (11), (12) i (13) określa wzór (19).

k_e = {8 \cdot \lambda \cdot \rho \cdot \ Q^3 \cdot k_j \over \pi^2 \cdot \eta } \cdot {1 \over d^5}    (19)

Obliczenia kosztów i średnic optymalnych dla różnych okresów eksploatacji zawiera arkusz kalkulacyjny:

Wyniki obliczeń przedstawiono na wykresie rys. 6. 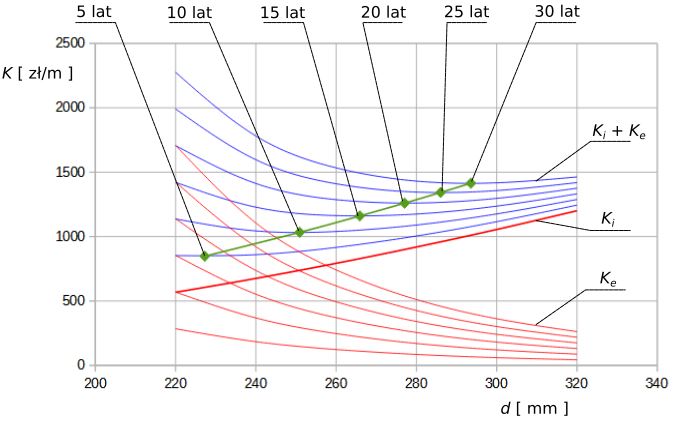Rys.6. Krzywe kosztów i średnica optymalna w zależności od czasu eksploatacji

5. Jednostkowy koszt eksploatacji, ze stopą dyskontowej r=5%

Planowane parametry pracy rurociągu.

    • Q = 150 m3/h – przepływ
    • kj = 1 zł/kWh – bieżący koszt jednostkowy energii

W przykładzie jak poprzednio uwzględniono jedynie koszty energii. W obliczeniach uwzględniono roczy okres obliczeniowy kosztów. Roczne jednostkowe koszty energii określa wzór (20).

k_r = k_e \cdot t = {8 \cdot \lambda \cdot \rho \cdot \ Q^3 \cdot k_j \over \pi^2 \cdot \eta } \cdot {1 \over d^5} \cdot  31536000 =    (20)

Przypominam - obliczenia prowadzimy w jednostkach SI, 1 rok = 31536000 s.

Koszt zdyskontowane energii na podstawie wzoru Koszt zdyskontowany (8) obliczamy ze wzoru (21).

k_i = {k_r \over (1 + r)^i}   (20)

Wartość NPV dla obliczamy przez sumowanie wartości Ki dla wybranego okresu eksploatacji.

NPV = \sum_{i=1}^n {k_i \over \left( 1 + r \right)^i}   (21)

Obliczenia kosztów zdyskontowanych r=5% i średnic optymalnych dla różnych okresów eksploatacji zawiera arkusz kalkulacyjny:

Wyniki obliczeń przedstawiono na wykresie rys. 7.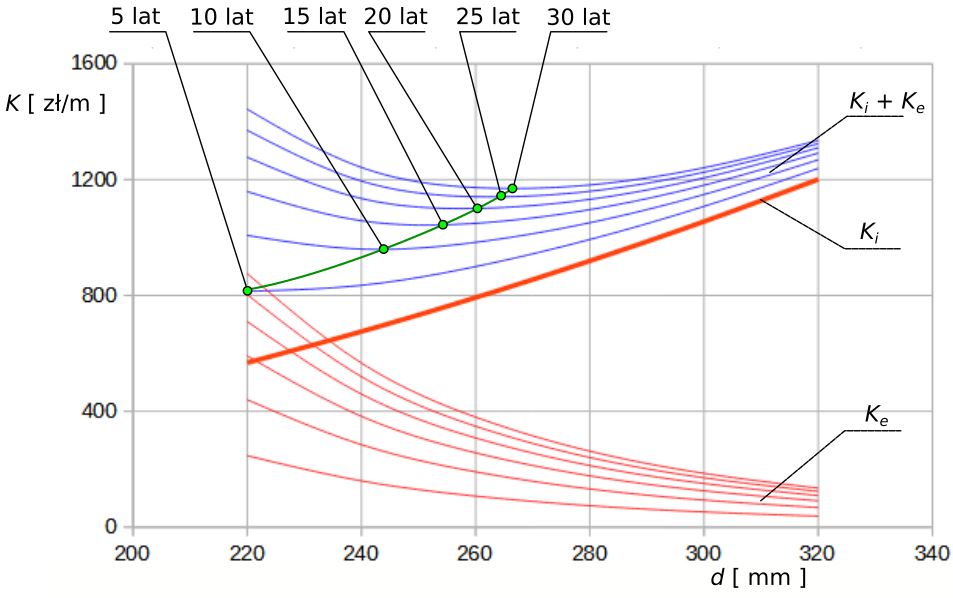

Rys.7. Średnica optymalna w zależności od czasu eksploatacji przy stopie dyskontowej 5%

6. Jednostkowy koszt eksploatacji, ze stopą dyskontową r=10%

Obliczenia kosztów zdyskontowanych r=10% i średnic optymalnych dla różnych okresów eksploatacji zawiera arkusz kalkulacyjny:

Wyniki obliczeń przedstawiono na wykresie rys. 8.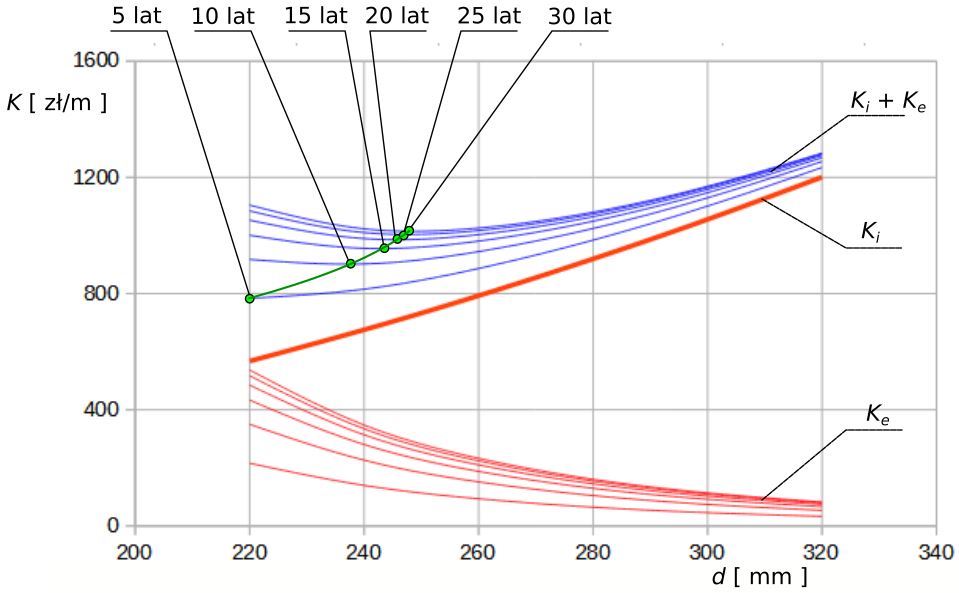

Rys.8. Średnica optymalna w zależności od czasu eksploatacji przy stopie dyskontowej 10%

PAMIĘTAJ !

  • Czas eksploatacji ma zasadniczy wpływ na optymalną średnicę
  • Stopa dyskontowa r ma wpływ na optymalną średnicę rurociągu
  • Z porównania wykresów na rys. 6, 7 i 8 wynika, że im wyższa stopa dyskontowa tym średnica optymalna rurociągu jest mniejsza
  • W układach mogą występować różne ograniczenia, np. minimalna prędkość przepływu, dla mieszanim.

Warto sprawdzić