Procent składany
Jeżeli mamy pewną kwotę np. PV0 = 1000 i założymy lokatę w banku np. na r = 5%, to po roku otrzymamy kwotę PV1, wyrażoną wzorem (1).
FV_1 = PV_0 \cdot (1+r) = 1000 \cdot 1,05 = 1050 (1)
Jeżeli lokatę przedłużymy na drugi rok to odsetki będą się składały z odsetek za pierwszy i drugi rok – stąd nazwa procent składany. Otrzymana kwota PV2, będzie wyrażona wzorem (2).
FV_2 = FV_1 \cdot (1+r) = PV_0 \cdot (1+i) \cdot (1+r) =1050 \cdot 1,05 = 1103 (2)
Jeżeli lokatę przedłużymy na kolejny rok, to otrzymamy kwotę PV3, wyrażoną wzorem (3).
FV_3 = FV_2 \cdot (1+r) = PV_0 \cdot (1+r) \cdot (1+r) \cdot (1+r) = 1103 \cdot 1,05 = 1158 (3)
Na podstawie wzorów (1), (2) i (3) możemy napisać ogólny wzór na procent składany (4)
FV = PV \cdot \left( 1 +r \right)^n (4)
PV - wartość bieżąca (present value) FV - nominalna wartość przyszła (future value) r - stopa procentowa, najczęściej roczna (interest rate) n - liczba okresów rozliczeniowych, najczęściej lat (number of times)
Na podstawie wzoru (4) możemy obliczyć stan konta w banku np. po 10 latach.
FV = PV \cdot \left( 1 + r \right)^n = 1000 \cdot 1,05^10 = 1629 (5)
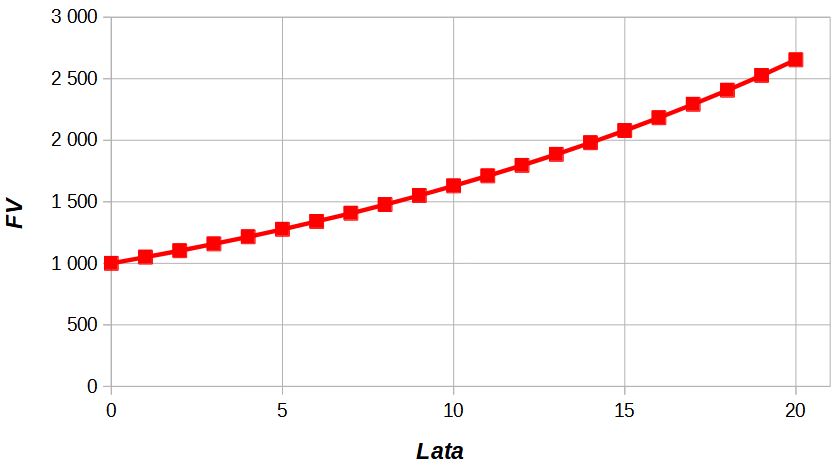
Rys. 1. Zmiana wartości FV z czasem przy stałej wartości i
Nie trudno zauważyć, że wartości PV i FV są różne i że dzisiejsze 1000 zł za 10 lat będzie więcej warte.
Koszt zdyskontowany
Przykład (5) prowadzi nas także do wniosku, że oszczędności i zyski oraz wydatki uzyskane lub poniesione w przyszłości mają inną wartość z dzisiejszego punktu widzenia. Koszt zdyskontowany (odniesiony do dziś), przyszłych oszczędności i strat, możemy obliczyć jako odwrotność procentu składanego (4).
PV = {FV \over \left( 1 + r \right)^n} (6)
Jeżeli planujemy, że za 10 lat, dzięki dzisiejszej inwestycji, zaoszczędzimy np. FV = 1000 i założymy stałą stopę dyskontową r = 10% (np. odpowiednik stopy oprocentowania kredytu w banku), to aktualną wartość oszczędności, „na dziś”, PV opisuje wzór (7).
PV = {FV \over \left( 1 + r \right)^n} = {1000 \over \left( 1 + 0,1 \right)^n} = 386 (7)
Wynik obliczeń (7) mówi nam, że przyszłe dochody mają znacznie mniejszą wartość, 386 << 1000.
Metoda NPV
W analizach technicznych w których koszty inwestycyjne i koszty eksploatacyjne mają istotny wpływ na parametry projektowanych obiektów, np. wielkość turbiny w elektrowni wodnej, średnica rurociągu itp., stosowane są wersje wzoru (6) uwzględniające zmianę zysków i strat w czasie, nazywane metodą NPV (net present value). Jeden z wariantów metody NPV, odpowiednią do oceny efektywności inwestycji przedstawia wzór (8).
NPV = \sum_{i=1}^n{\left({R_i - (I_i + O_i + M_i)} \over \left( 1 + r_i \right)^n \right)} + V_r (8)
NPV – wartość bieżąca (net present value) n – liczba okresów rozliczeniowych, najczęściej lat
Vr – wartość końcowa inwestycji (residual value) Wartości w i-tym okresie rozliczeniowym Ri – przychody (revenues in period) Ii – inwestycje (investment in period) Oi – koszty operacyjne (np. koszty kredytu) (operating costs in period) Mi – koszty eksploatacyjne (operating costs in period) ri – okresowa stopa dyskontowa, najczęściej roczna
W przypadku występowania inflacji, realną stopę dyskontową obliczamy ze wzoru (9).
r ={1+r_n \over 1+ i} - 1 (9)
r – realna stopa dyskontowa rn – nominalna stopa dyskontowa i – inflacja
PAMIĘTAJ !
- Analiza kosztów to banalnie proste obliczenia – popatrz na przykłady
- Obliczenia prowadź w jednolitym układzie jednostek (procent % jest spoza układu)
- Bank nic nie produkuje!
- Oprocentowanie lokaty w banku jest mniejsze od oprocentowania kredytu, bo z tej różnicy finansujesz bank i bankierów.
- Jeżeli chcesz finansować inwestycję z kredytu to stopa dyskontowa musi być większa od stopy oprocentowania kredytu, bo z twojego zysku musisz utrzymać firmę, bank i bankierów
- Jeżeli masz dobry pomysł to zainwestuj swoje pieniądze – nie będziesz utrzymywać banku i bankierów
Warto sprawdzić
- Optymalna średnica rurociągu
- Obliczenia optymalnej średnicy rurociągu