Projekt wirnika odśrodkowego cz. 2 – obliczenia części przepływowej

Kontynuacja obliczeń z cz.1 – obliczenia wstępne

6. Obliczenie średnicy wału i średnicy piasty

6.1. Nominalna prędkość kątowa silnika

$\omega = {2930 \cdot 2 \cdot \pi \over 60} = 306,8 \ 1/s$

6.2. Moment nominalny silnika

$M_n = {P \over \omega} = {1100 \over 306,8} = 35,85 \ Nm$

6.3. Maksymalny moment silnika

Maksymalny moment na wale pompy wystąpi podczas każdego rozruchu pompy, tuż przed osiągnięciem nominalnej prędkości obrotowej (moment pompy = moment silnika).

Do wyznaczenia maksymalnego moment wykorzystamy krotność moment M_max/M_n.

$M_{max} = M_n \cdot \left( {M_{max} \over M_n} \right) = 35,85 \cdot 2,9 = 103,97$

6.4. Średnica rdzenia wału

Na tym etapie projektu nie znamy schematu obciążenia wału. W tej sytuacji, zakładam, że średnicę rdzenia wału można oszacować na podstawie obciążeń skręcających.

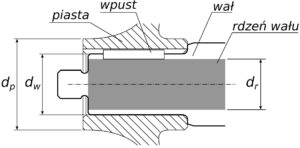
Rys.1. Schemat obliczeniowy średnicy rdzenia wału

Dopuszczalne naprężenia skręcające wału określa wzór:

$k_s > {M \over W_o}$

Wskaźnik wytrzymałości na skręcania, wału o przekroju kołowym, opisuje wzór:

$W_o = {\pi \cdot d^3 \over 16}$

Po połączeniu równania na naprężenia i wskaźnik otrzymamy wzór na minimalną średnicę rdzenia wału:

$d_r \ge \sqrt[3]{16 \cdot M \over \pi \cdot k_s}$

d_r - średnica wału
M - moment obciążenia wału
W_o - wskaźnik wytrzymałości na skręcanie
k_s - dopuszczalne naprężenia skręcające

$d_r \ge \sqrt[3]{16 \cdot M_{max} \over \pi \cdot k_{sj}}$

Na wał wybieram stal zwykłej jakości S275

$Re = 275 MPa$

Dopuszczalne naprężenia skręcające stali S175

$k_s = 0,33 \cdot Re = 0,33 \cdot 175 = 90,7 \ MPa$

Minimalna średnica wału

$d_r \ge \sqrt[3]{16 \cdot M \over \pi \cdot k_s} = \sqrt[3]{16 \cdot 103,97 \over \pi \cdot 90,7 e^6} = 0,018$

6.5. Średnica wału

Moment z wału na piastę wirnika będzie przenoszony poprzez połączenie wpustowe.

Na podstawie Poradnika mechanika s. 240, dla średnicy wału 18mm dobieram wpust a x b = 6 x 6.

Zgodnie z zaleceniami Mazanek E. – Przykłady obliczeniowe z podstaw konstrukcji maszyn s. 369 rys.9.4.3, zwiększam średnicę wału o wysokość wpustu.

$d_{w min} = d_r + 0,006 = 0,024$

Wybieram, pierwszą, większą, znormalizowaną średnicę wału.

$d_w = 0,025 = 25 \ mm$

6.6. Średnica piasty wirnika

Ze względów wytrzymałościowych i konieczności zmieszczenia rowka na wpust, zakładam, że średnica piasty d_p będzie większa o 40% od średnicy wału, patrz rys.1.

$d_p = 1,4 \cdot d_w = 1,4 \cdot 0,025 = 0,035 = 35mm$

7. Obliczenie średnicy wlotu

7.1. Obliczenia sprawności objętościowej

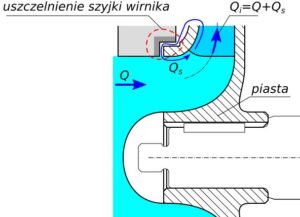
Rys.1. Schemat obliczeniowy przepływu wewnętrznego

Sprawność objętościowe na podstawie wzoru Łomakina

$\eta_V = {1 \over 1+0,287 \cdot n_q^{-2/3}}={1 \over 1+0,287 \cdot 18,49^{-2/3}} = 0,961$

7.2. Obliczenia przepływu wewnętrznego

$Q_i = {Q \over \eta_V} = {0,0139 \over 0,961} = 0,01446 = 52,05 m^3/h$

7.3. Prędkość merydionalna na wlocie

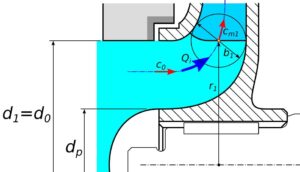
Rys.2. Wlot do wirnika

Prędkość merydionalną na wlocie c_m1 można obliczyć ze wzoru:

$c_{m1} = K_{cm1} \cdot \sqrt {2g \cdot H}$

Wartość współczynnika prędkości merydionalnej, na podstawie wykresu Stepanoffa, wynosi:

$K_{cm1} = 0,129 \ \ \ dla \ n_q=18,49$

Prędkość merydionalna na wlocie

$c_{m1} = K_{cm1} \cdot \sqrt {2g \cdot H} = 0,129 \cdot \sqrt {2 \cdot 9,81 \cdot 50} = 4,07$

7.4. Obliczenia średnicy szyjki wirnika

Prędkość w szyjce wirnika

$c_0 = 0,9 \cdot c_{m1} = 0,9 \cdot 4,07 = 3,66$

Pole przekroju wlotowego, na podstawie równania ciągłości

$A_0 = {Q_i \over c_0} = {0,01446 \over 3,66} = 0,003946$

Pole przekroju piasty

$A_p = {\pi \cdot d_p^2 \over 4} = {3,14 \cdot 0,035^2 \over 4} = 0,000962$

7.5. Wybór średnicy wlotowej

Średnica wlotowa wirnika

$d_0 = \sqrt {4 \cdot (A_0 + A_p) \over \pi} = 0,0791 = 79,1mm$

Wybór średnicy wlotowej pompy zgodnej z szeregiem średnic nominalnych rurociągów DN.

DN – 10, 15, 20, 32, 40, 50, 65, 80, 100, 125, 150, 200, 250, 300, 350, 400, 450, 500

Wybieram średnicę DN – 80.

Przyjmuje rzeczywistą średnicę przekroju wlotowego

d0 = 0,08

Zakładam, że średnica wlotu d1 będzie równa średnicy szyjki wirnika d0

d1= d0 = 0,08

8. Obliczenie kąta łopatki na wlocie

8.1. Obliczenia kata łopatki na wlocie

Prędkość obwodowa na wlocie

$u_1 = r_1 \cdot \omega = {0,08 \over 2} \cdot 306,8 = 12,27$

Zakładam, że napływ na wirnik jest bez zawirowania wstępnego co oznacza, że kąt napływu cieczy α₁ = 90°, a wektor c₁ pokrywa się z wektorem c_m1.

Obliczeniowy kąt łopatki na wlocie (kąt bezuderzeniowy)

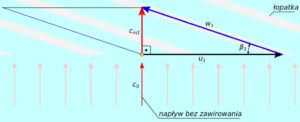
Rys.3. Trójkąt prędkości na wlocie

$\beta_1 = arctg \left({c_{m1} \over u_1} \right) = arctg \left({4,07 \over 12,27} \right) = arctg (0,3317) = 0,3203 = 18,35^\circ$

8.2. Obliczenia kata konstrukcyjnego łopatki na wlocie

Kąt natarcia na wlocie

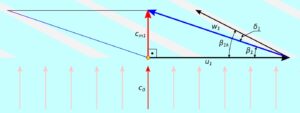
Rys.4. Trójkąt prędkości na wlocie z uwzględnieniem kąta natarcia

Przyjmuje kąt natarcia wg, zaleceń A. Misiewicza

$\delta_1 = 22,75 \cdot n_q^{-04581} = 5,98^\circ$

Kąt konstrukcyjny łopatki

$\delta_{1k} = \beta_1 + \delta_1 = 18,35 + 5,98 = 24,33^\circ$

Ostatecznie przyjmuję zaokrągloną wartość kąta łopatki na wlocie

$\delta_{1k} = 24^\circ = 0,419 rad$

8.3. Wybór technologii wykonania wirnika i liczby łopatek

Na wybór liczby i grubości łopatek decydujący wpływ ma materiał i technologia wykonania wirnika,

Popularne materiały

żeliwo,
staliwo,
brąz,
stal nierdzewna,
aluminium,
tworzywa sztuczne.

Popularne technologie

odlewanie,
tłoczenie z blachy,
spawanie/zgrzewanie,
klejenie,
formowanie wtryskowe,
skrawane.

Wybieram wirnik z żeliwa, wykonany w technologii odlewania.

Grubość łopatki

S = 0,004 = 4mm

Grubość łopatki na wlocie

S1 = 0,003 = 3mm

Liczba łopatek wirników odśrodkowych wynosi Z = 5 ÷ 9.

Przyjmuję liczbę łopatek

Z = 7

9. Obliczenia szerokości kanału na wlocie

9.1. Współczynnik przesłonięcie przekroju na wlocie

Podziałka na wlocie

t_1 = {\pi \cdot d_1 \over Z} = {3,14 \cdot 0,08 \over 7} = 0,0359

Rzut grubości łopatki na kierunek unoszenia

s_{u1} = {s_1 \over sin(\beta_{1k})} = {0,003 \over sin(0,419)} = 0,0737

Współczynnik przesłonięcia wlotu

\varphi_1 = {t_1 \over t_1 - s_{u1}} = {0,0359 \over 0,0359 - 0,00737} = 1,259

9.2. Szerokość kanału na wlocie

Pole przekroju wlotowego

A_1 = {Q_i \cdot \varphi_1 \over c_{m1}} = {0,01445 \cdot 1,259 \over 4,07} = 0,004469

Szrokość wirnika na wlocie

b_1 = {A_1 \over \pi \cdot d_1} = {0,004469 \over 3,14 \cdot 0,08} =0,01776

Przyjmuję szerokość na wlocie

b₁ = 0,018 = 18mm

10. Obliczenie średnicy i szerokości wirnika na wylocie

10.1. Podstawowe parametry wirnika

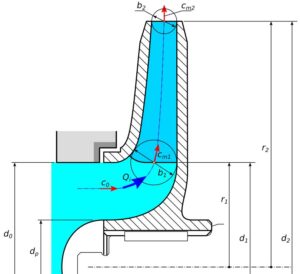
Rys. 4. Przekrój merydionalny wirnika

10.2. Obliczenia poprawki Pfleiderera

Wykonamy obliczenia średnicy wylotu wirnika dla 4 wartości kąta wylotowego łopatki.

β_{2 27} = 27°
β_{2 30} = 30°
β_{2 33} = 33°
β_{2 36} = 36°

Teoretyczną wysokość podnoszenia pompy wyznaczymy na podstawie równania Eulera i poprawki Pfleiderera.

Poprawka p jest zdefiniowana wzorem 9.

$p={\chi \cdot r_2^2 \over Z \cdot M_{st}}$ (9)

p - poprawka Pfleiderera
χ - współczynnik doświadczalny 
r₂ - promień wirnika na wylocie
Z - liczba łopatek
M_st - moment statyczny środkowej linii prądu

Oszacowanie współczynnika χ wg. C. Pfleiderera dla odprowadzenia cieczy do spiralnego kanału zbiorczego.

$\chi = 0,65 \cdot \left(1+{ \beta_2 \over 60} \right)$

$\chi_{27} = 0,65 \cdot \left(1+{ 27 \over 60} \right) = 1,02$
$\chi_{30} = 0,65 \cdot \left(1+{ 30 \over 60} \right) = 1,05$
$\chi_{33} = 0,65 \cdot \left(1+{ 33 \over 60} \right) = 1,09$
$\chi_{36} = 0,65 \cdot \left(1+{ 36 \over 60} \right) = 1,12$

Poprawka Pfleiderera dla wirnika odśrodkoweg

$p = {2 \cdot \chi \over Z} \cdot {1 \over 1 - \left(d_1 \over d_2 \right)^2}$

Wartości średnicy wlotu i wylotu na podstawie punktów 7.3 i 4.5.

$p_{27} = {2 \cdot 1,02 \over 7} \cdot {1 \over 1 - \left( 0,08 \over 0,203 \right)^2} = 0,343$
$p_{30} = {2 \cdot 1,05 \over 7} \cdot {1 \over 1 - \left( 0,08 \over 0,203 \right)^2} = 0,355$
$p_{33} = {2 \cdot 1,09 \over 7} \cdot {1 \over 1 - \left( 0,08 \over 0,203 \right)^2} = 0,367$
$p_{36} = {2 \cdot 1,12 \over 7} \cdot {1 \over 1 - \left( 0,08 \over 0,203 \right)^2} = 0,378$

10.3. Oszacowanie sprawności hydraulicznej

Obliczenia średnicy zredukowanej na wlocie wg. Suchanowa

$d_{1zr} = 4000 \cdot \sqrt[3]{Q \over n} = 4000 \cdot \sqrt[3]{0,0139 \over 2930} = 67,2mm$

Obliczenia sprawności hydraulicznej wg. Łomakina

$\eta_h = 1 - {0,42 \over \left( log(d_{1zr}) - 0,172 \right)^2} = 1 - {0,42 \over \left( log(67,2) - 0,172 \right)^2} = 0,846$

Q - wydajność pompy m3/s
n - prędkość obrotowa obr/min
d_1zr - średnica zredukowana mm

10.4. Obliczenia prędkości merydionalnej na wylocie

Prędkość merydionalną na wlocie c_m2 można obliczyć ze wzoru:

$c_{m2} = K_{cm2} \cdot \sqrt {2g \cdot H}$

Wartość współczynnika prędkości merydionalnej, na podstawie wykresu Stepanoffa, wynosi:

$K_{cm2} = 0,10 \ \ \ dla \ n_q=18,49$

Prędkość merydionalna na wlocie

$c_{m2} = K_{cm2} \cdot \sqrt {2g \cdot H} = 0,1 \cdot \sqrt {2 \cdot 9,81 \cdot 50} = 3,12$

10.5. Obliczenia prędkości obwodowej na wylocie

$u_2 = {c_{m2} \over 2 \cdot tg \beta_2} + \sqrt {\left( c_{m2} \over 2 \cdot tg \beta_2 \right)^2 + {g \cdot H \cdot (1 + p) \over \eta_h}}$

$u_{2 \ 27} = {3,12 \over 2 \cdot tg 27} + \sqrt {\left( 3,12 \over 2 \cdot tg 27 \right)^2 + {g \cdot H \cdot (1 + 0,343) \over 0,846}} = 31,12$
$u_{2 \ 30} = {3,12 \over 2 \cdot tg 30} + \sqrt {\left( 3,12 \over 2 \cdot tg 27 \right)^2 + {g \cdot H \cdot (1 + 0,355) \over 0,846}} = 30,85$
$u_{2 \ 33} = {3,12 \over 2 \cdot tg 33} + \sqrt {\left( 3,12 \over 2 \cdot tg 27 \right)^2 + {g \cdot H \cdot (1 + 0,367) \over 0,846}} = 30,65$
$u_{2 \ 36} = {3,12 \over 2 \cdot tg 36} + \sqrt {\left( 3,12 \over 2 \cdot tg 27 \right)^2 + {g \cdot H \cdot (1 + 0,378 \over 0,846}} = 30,49$

10.6. Obliczenia i wybór średnicy wirnika na wylocie

$d_2 = 2 \cdot {u_2 \over \omega}$

$d_{2 \ 27} = 2 \cdot {31,12 \over 306,8} = 0,203$
$d_{2 \ 30} = 2 \cdot {30,85 \over 306,8} = 0,201$
$d_{2 \ 33} = 2 \cdot {30,65 \over 306,8} = 0,200$
$d_{2 \ 36} = 2 \cdot {30,49 \over 306,8} = 0,199$

Wybieram kąt łopatki β₂ = 33º i średnicę d₂ = 0,2 = 200mm

10.7. Obliczenia szerokości wylotu

Obliczenia są prowadzone podobnie jak w punkcie 9.

Podziałka na wylocie

$t_2 = {\pi \cdot d_2 \over Z} = {3,14 \cdot 0,2 \over 7} = 0,0896$

Rzut grubości łopatki na kierunek unoszenia

$s_{u2} = {s_2 \over sin(\beta_2)} = {0,004 \over sin(33)} = 0,0734$

Współczynnik przesłonięcia wylotu

$\varphi_2 = {t_2 \over t_2 + s_{u2}} = {0,0896 \over 0,0896 - 0,00734} = 1,089$

Pole przekroju wylotowego

$A_2 = {Q_i \cdot \varphi_2 \over c_{m2}} = {0,01445 \cdot 1,089 \over 3,12} = 0,00505$

Szerokość wirnika na wylocie

$b_2 = {A_2 \over \pi \cdot d_2} = {0,00505 \over 3,14 \cdot 0,2} =0,00805$

Przyjmuję szerokość wirnika na wylocie

b2 = 0,008 = 8mm

PAMIĘTAJ !

To jest ćwiczenie dla studentów a nie „prawdziwy projekt”

Warto sprawdzić: