Poprawka Pfleiderera

Punktem wyjścia jest równanie Eulera, przy założeniu nieskończonej liczby nieskończenie cienkich łopatek.

H_{th \infty}={1 \over g} \cdot (u_2 \cdot c_{u2 \infty} - u_1 \cdot c_{u1}) (1)

Zwykle dopływ do pompy nie ma zawirowania wstępnego, więc c1 jest prostopadłe do u1, a cu1 = 0, patrz rys.1.

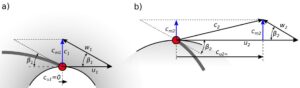
Rys.1. Trójkąty na wlocie i wylocie wirnika

Hth∞- wysokość podnoszenia przy nieskończonej licznie nieskończenie cienkich łopatek
c1 - prędkość bezwzględna na wlocie
u1 - prędkość unoszenia na wlocie 
um1 - prędkość merydionalna na wlocie 
cu1 - rzut prędkości bezwzględnej na kierunek prędkości unoszenia na wlocie
β1 - kąt łopatki na wlocie
c2 - prędkość bezwzględna na wylocie
c2∞ - prędkość bezwzględna na wylocie, przy nieskończonej licznie nieskończenie cienkich łopatek
u2 - prędkość unoszenia na wylocie 
cm2 - prędkość merydionalna na wylocie 
cu2 - rzut prędkości bezwzględnej na kierunek prędkości unoszenia na wylocie, przy skończonej licznie łopatek 
cu2∞ - rzut prędkości bezwzględnej na kierunek prędkości unoszenia na wylocie, przy nieskończonej licznie nieskończenie cienkich łopatek
β2 - kąt łopatki na wylocie

Wstawiamy wartość cu1 do równania Eulera 1.

H_{th \infty}={1 \over g} \cdot (u_2 \cdot c_{u2 \infty} - u_1 \cdot 0) (2)

Ostatecznie równanie Eulera redukuje się do postaci 3.

H_{th \infty} = {u_2 \cdot c_{u2 \infty} \over g} (3)

Badanie przebieg chakterystyki Hth∞, w funkcji wydajności, na podstawie równania 3 prowadzi kolejno do następujących wniosków:

  • prędkość unoszenia jest wartością stałą większą od zera – u_2 = r_2 \cdot \omega = const > 0 bo r_2 = const > 0 i \omega = const > 0
  • kąt łopatki jest wartością stałą β2
  • zmiana wysokości podnoszenia Hth∞ następuje wyłącznie z powodu zmiany wartości rzutu prędkości bezwzględnej na kierunek prędkości unoszenia cu2
  • wydajność pompy jest opisana zależnością Q=A \cdot c_m
  • dla wylotu, wydajność pompy jest opisana zależnością Q=\pi \cdot d_2 \cdot b_2 \cdot c_{m2}
  • wydajność pompy Q zmienia się na skutek zmiany wartości cm2 bo d_2=const>0 i b_2=const>0
  • przy zerowej wydajności Q=0, prędkość merydionalna i kąt prędkości bezwzględnej mają wartość zero cm2 = 0, α2=0, a prędkość bezwzględna pokrywa się z prędkością unoszenia c2 ≡ u2
  • przy zerowej wysokości podnoszenia Hth∞=0 prędkość bezwzględna jest prostopadła do prędkości unoszenia α2=90°

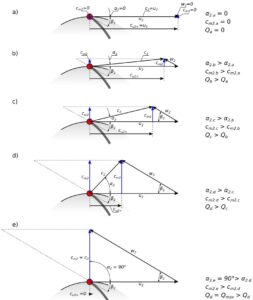
Rys.2. Zmiana trójkąta prędkości na wylocie przy zmianie wydajności pompy

Tak więc, przy zerowej wydajności Q=0 wysokość podnoszenia wynosi:

H_{th \infty} = {u_2 \cdot u_2 \over g} = {u_2^2 \over g}

oraz, przy zerowej wysokości podnoszenia Hth∞=0 prędkość merydionalna i wydajność wynosi:

c_{m2} = {u_2 \cdot tg(\beta_2)} (4)

Q_{th \infty} = \pi \cdot d_2 \cdot b_2 \cdot u_2 \cdot tg(\beta_2) (5)

Q - wydajność pompy
ω - prędkość kątowa wirnika 
r2 - promień wirnika na wylocie
d2 - średnica wirnika na wylocie
b2 - szerokość wirnika na wylocie
ρ - gęstość cieczy
g - przyśpieszenie ziemskie
α2 - kąt prędkości bezwzględnej na wylocie

Na podstawie tych dwóch punktów, możemy narysować teoretyczną charakterystykę przepływu pompy przy nieskończonej liczby nieskończenie cienkich łopatek rys.3.a.

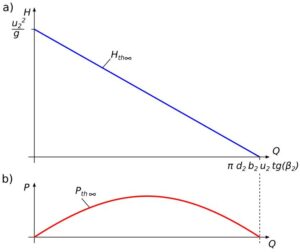
Rys.3. Charakterystyka pompy przy nieskończonej liczbie łopatek

Teoretyczna charakterystyka przepływu Hth∞, rys 3.a, jest podstawą określenia teoretycznej charakterystyki mocy hydraulicznej pompy Pth∞, rys.3.b. Do obliczeń jej przebiegu wykorzystujemy wzór 6.

P_{th \infty} = Q \cdot H_{th \infty} \cdot \rho \cdot g (6)

Charakterystyka przepływu Hth∞(Q) określa ile energii są w stanie przekazać cieczy łopatki wirnika, gdy jest ich nieskończenie wiele (dużo).

Pytanie brzmi: ile energii jest w stanie przekazać mniejsza – skończona liczba łopatek?

Proponuję wykonanie prostego doświadczenia, z talerzem zupy, pokazanego na filmie 1.

Film 1. Zupa

Z przeprowadzonego eksperymentu wynika, że przy obrocie:

  • ciecz nie obraca się, względem stołu – układu bezwzględnego
  • ciecz obraca się w odwrotnym kierunku, względem talerza – układu ruchomego

 

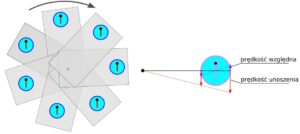
Rys.3. Prędkość względna wywołana wirowaniem obudowy

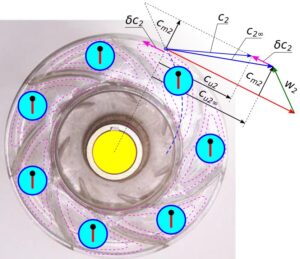
Rys.4. Zmiana prędkości bezwzględnej c2 i jej rzutu cu2 na wylocie przy skończonej liczbie łopatek

Przy skończonej liczby łopatek w przestrzeni międzyłopatkowej tworzy się wir, który zmniejsza wartość rzutu prędkości bezwzględnej na kierunek unoszenia na wylocie o wartość prędkość krążenia δc2, z cu2∞ na cu2. Powoduje to zmniejszenie możliwości przekazywania energii przez wirnik, co jest opisane równaniem 7.

H_{th} = {u_2 \cdot c_{u2} \over g} (7)

Carl Pfleiderer zaproponował aby wpływ skończonej liczby łopatek – stosunek spadku wysokości podnoszenia Hth∞ – Hth do teoretycznej wysokości podnoszenia Hth opisać stałym współczynnikiem p.

{H_{th \infty} - H_{th} \over H_{th}} = p (8)

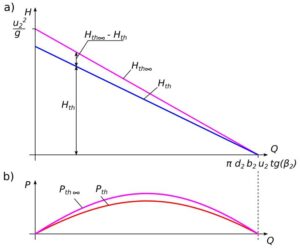
Rys.5. Charakterystyka pompy przy nieskończonej liczbie łopatek

Poprawka p została zdefiniowana, przez autora wzorem 9.

p={\chi \cdot r_2^2 \over Z \cdot M_{st}} (9)

p - poprawka Pfleiderera
χ - współczynnik doświadczalny 
r2 - promień wirnika na wylocie
Z - liczba łopatek
Mst - moment statyczny środkowej linii prądu

Wartości współczynnika \chi wg. C. Pfleiderera

  • \chi = 0,6 \cdot \left( 1+ {\beta_2 \over 60} \right) – wypływ do kierownicy odśrodkowej
  • \chi = \left( 0,65 \div 0,85 \right) \cdot \left( 1+ {\beta_2 \over 60} \right) – wypływ do spirali
  • \chi = \left( 0,85 \div 1,0 \right) \cdot \left( 1+ {\beta_2 \over 60} \right) – wypływ do kierownicy bezłopatkowej

Zalecane wartości współczynnika χ wg. analizy W. Jędrala

  • \chi = \left( 0,55 \div 0,68 \right) + 0,6 \cdot sin \left( \beta_2 \right) – dla d_2 / d_1 \ge 2
  • \chi = \left( 1,0 \div 1,2 \right) \cdot \left(1+ sin \left(\beta_2 \right) \right) – dla d_2 / d_1 < 2

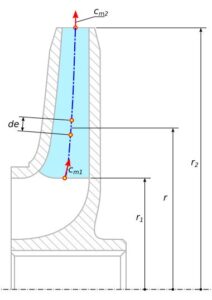
Rys.5. Moment statyczny średniej linii prądu

Moment statyczny środkowej linii prądu względem osi obrotu jest zdefiniowany wzorem 10.

M_{st} = \int_{r_1}^{r_2} r \cdot de (10)

Jeżeli mamy określone współrzędne punktów opisujących środkową linię prądu, wówczas moment statyczny możemy obliczyć z wykorzystaniem arkusza kalkulacyjnego Excel lub Calc.

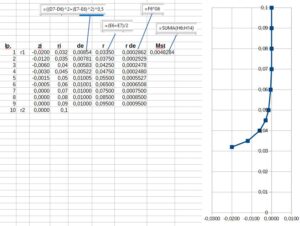
Rys.6. Przykład obliczenia momentu statycznego w arkuszu kalkulacyjnym

Dla wirnika odśrodkowego, środkowa linia prądu jest niemal odcinkiem prostym, prostopadłym do osi obrotu. W tym przypadku możemy moment statyczny obliczyć z uproszczonej formuły 11.

Odległość od osi obrotu – promień odcinka:

r = {r_2 + r_1 \over 2}

Długość odcinaka:

de = r_2 - r_1

M_{st} = r \cdot de = {\left( r_2 + r_1 \right) \cdot \left( r_2 - r_1 \right) \over 2} = {r_2^2 - r_1^2 \over 2} (11)

Po podstawieniu wyrażenia 11 do równania 9 otrzymamy wzór na poprawkę dla pompy odśrodkowej 12.

p={2 \cdot \chi \cdot r_2^2 \over Z \cdot \left(r_2^2 - r_1^2 \right)} = {2 \cdot \chi \over Z} \cdot {1 \over 1 - \left(r_1^2 \over r_2^2 \right)^2} = {2 \cdot \chi \over Z} \cdot {1 \over 1 - \left(d_1^2 \over d_2^2 \right)^2} (12)

PAMIĘTAJ !

Warto sprawdzić: