Przy projektowania układu transportu cieczy rurociągiem, często zadajemy sobie pytanie: jaką wybrać średnicę? Jaka średnica zapewni minimalizację kosztu transportu?
W przeprowadzonej analizie wyodrębnimy dwa czynniki: koszt budowy rurociągu oraz koszt energii potrzebny na przetransportowanie cieczy.
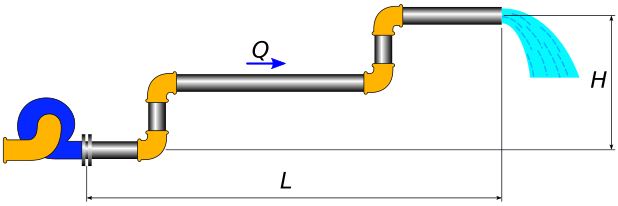
Rys. 1. Układ transportu rurowego
Q - przepływ L - długość rurociągu H - geometryczna wysokość podnoszenia
Koszt inwestycyjny
Założenia metody szacowania kosztów rurociągu:
- ciśnienie nominalne rurociągu jest stałe
- materiał rurociągu ma stałą wytrzymałość
- cena 1mb rury jest proporcjonalna do ilości materiału rurociągu
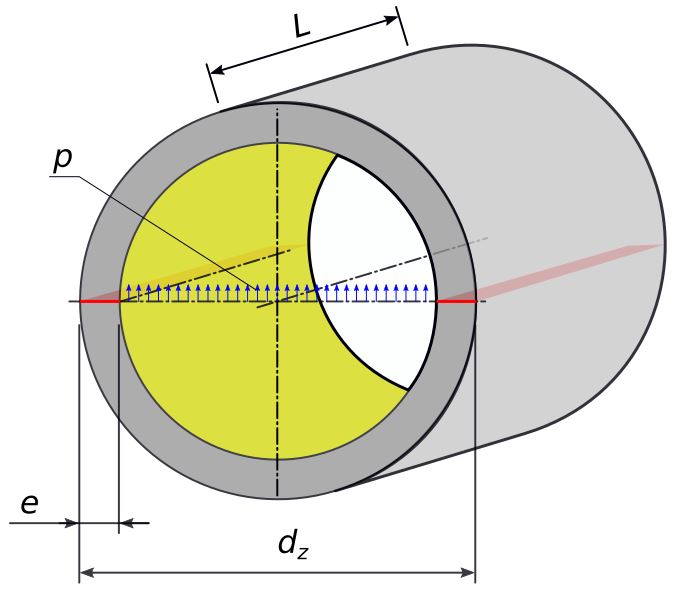
Rys. 2. Parametry rurociągu
Naprężenia w rurociągu wywołane ciśnieniem pracy, z pominięciem naprężeń wzdłużnych, można oszacować ze wzoru (1).
\sigma = {F \over A} = {L \cdot d \cdot p \over L \cdot 2 \cdot e} = {d \cdot p \over 2 \cdot e} (1)
Zgodnie z założeniami p = const i \sigma = const. Na tej podstawie wzór 1 możemy przekształcić do postaci (2).
const = {d \over e} (2)
Oznacza to, że dla stałego ciśnieniu pracy rurociągu (np. PN16 = 16 bar) rura będzie miała także stałe SDR (np. d/e = 11).
Przybliżoną masę materiału rurociągu i masę jednostkową określają wzory 3 i 4.
m = {\pi \cdot d \cdot e \cdot L \cdot \rho} (3)
{m \over L} = {\pi \cdot d \cdot e \cdot \rho} (4)
Ponieważ, na podstawie wzoru (2), dla stałych p i \sigma, grubość cienki e jest proporcjonalna do średnicy d, możemy wzór (4) przekształcić do postaci (5).
{m \over L} = \pi \cdot d \cdot {d \cdot p \over 2 \cdot \sigma} \cdot \rho = {\pi \cdot p \cdot \rho \over 2 \cdot \sigma} \cdot d^2 (5)
L - długość rurociągu dz - średnica zewnętrzna rurociągu e - grubość ścianki p - ciśnienie F - siła A - pole powierzchni σ - naprężenia rozciągające ρ - gęstość materiału rury
Ze wzoru (5), przy przyjętych założeniach wynika, że ilość materiału rurociągu, a zatem i jego cena jednostkowa powinna być proporcjonalna do kwadratu średnicy.
Na rys. 3 przedstawiono tabelę wymiarów rurociągów oferowanych na runku.
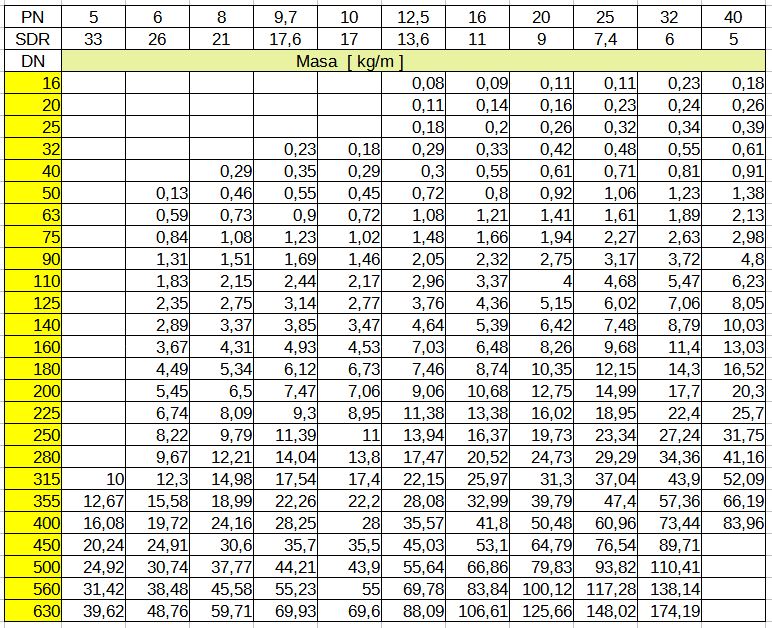
Rys. 3. Masa jednostkowa rur wykonanych z PE-HD
Na podstawie kolumny PN16 (SDR11) sporządzono wykres masy jednostkowej rurociągu, pokazany na rys.4.
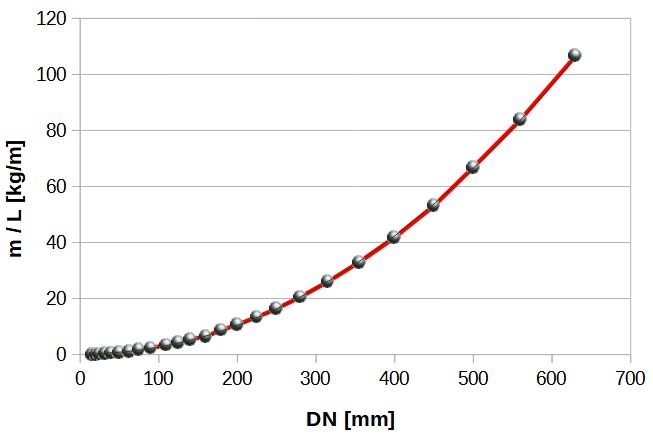
Rys. 4. Zmiana masy jednostkowej rury PN16
Na podstawie wniosków wyciągniętych ze wzoru (5), oraz wykresu na rys. 4 można przyjąć, że jednostkowe koszty zmienne (koszt wybudowania 1 m rurociągu) kz zmieniają się z kwadratem średnicy rurociągu.
Da kosztów zmiennych zaliczamy:
-
- zakup rury
- izolacja rurociągu
- złącza i armatura
- montaż rurociągu
- udźwig sprzętu
- robocizna
- koszt obsługi kredytu
- itp.
Przy budowie rurociągu występuje także pewna część kosztów, które nie zależą od średnicy. Da kosztów stałych ks możemy zaliczyć:
-
- koszt obliczeń hydraulicznych
- koszt projektu
- koszt pozwoleń
- koszt nadzoru
- itp.
Tak więc, można przyjąć, że koszt inwestycyjny Ki (koszt budowy rurociągu) składa się z: kosztu stałego ks oraz kosztu zmiennego kz który rosnie wraz ze średnicą rurociągu i można być opisać wzorem (6).
K_i = L \cdot \left( k_s + k_z \right) (6)
W modelu przyjęto, że koszty projektu i pozwoleń są proporcjonalne do długości rurociągu.
Na podstawie: analizy aktualnych danych cennikowych i rzeczywistych kosztów budowy innych rurociągów oraz równań (5) i (6), można stworzyć zależność opisującą przebieg zmian kosztów budowy rurociągu Ki , w postaci (7).
K_i = L \cdot \left( k_s + {k_0 \over d_0^2} \cdot d_{opt}^2 \right) (7)
Ki - koszty inwestycyjne L - długość rurociągu kz - jednostkowe koszty zmienne
ks - jednostkowe koszty stałe ko - koszty zmienne rurociągu (koszty odniesienia) do - średnica odniesienia dopt - optymalna średnica rurociągu
Dokładność obliczeń kosztów inwestycyjnych Ki będzie tym większa, im średnica rurociągu, dla którego określono koszt zakupu (średnica odniesienia), jest bliższa wyznaczonej średnicy optymalnej.
Koszt energii
Koszt energii, zużywanej na przetransportowanie cieczy rurociągiem, możemy opisać wzorem:
K_e = P_{el} \cdot t \cdot k_j = {P_h \cdot t \over \eta} \cdot k_j (8)
Ke - koszty energii [ zł ], Pel - moc elektryczna pobierana z sieci [ kW ], t - czas eksploatacji układu [ godz ], kj - koszt jednostkowy energii [ zł/kWh ], Ph - moc hydrauliczna strat [ kW ], η - sprawność agregatu (silnik + pompa).
Moc hydrauliczna, występująca we wzorze (8), może być obliczona na podstawie planowanego natężenia przepływu i oszacowanego przyrostu ciśnienia w pompie (9).
P_h = Q \cdot p = Q \cdot H \cdot \rho \cdot g = Q \cdot \left( H_g + \Delta H_s \right) \cdot \rho \cdot g (9)
Q - natężenie przepływu p - ciśnienie w rurociągu H - wysokość podnoszenia Hg - geometryczna wysokość podnoszenia ΔHs - wysokość strat w rurociągu ρ - gęstość cieczy
Zakłądamy, że straty miejscowe są znacznie mniejsze od strat liniowych, wzór (10),
\Sigma \zeta << \lambda \cdot {L \over d} (10)
Wysokość strat ciśnienia w układzie, możemy obliczyć ze wzoru Darcy-Weisbacha , który, po przekształceniach, zapisujemy w postaci (11).
\Delta H_s = {8 \cdot \lambda \cdot L \cdot Q^2 \over g \cdot \pi^2} \cdot {1 \over d_{opt}^5} (11)
ΔHs - straty hydrauliczne w rurociągu, λ - współczynnik strat liniowych, L - długość rurociągu, Q - natężenie przepływu, d - optymalna średnica rurociągu.
Jak wynika z analizy wzoru (11), straty hydrauliczne, a zatem i straty energii na pompowanie rosną z odwrotnością piątej potęgi średnicy rurociągu.
Energię elektryczną potrzebną do przepompowania cieczy w określonym czasie t opisuje wzór (12).
E_{el} = {Q \cdot (H + \Delta H_s) \cdot \rho \cdot g \over \eta} \cdot t (12)
Koszt energii koniecznej do transportu cieczy określa wzór (13)
K_e = E_{el} \cdot t (13)
Eel - energia elektryczna
Q - przepływ
H - geometryczna wysokość podnoszenia
ΔHs - straty hydrauliczne w rurociągu
ρ - gęstość cieczy
g - przyśpieszenie ziemskie
η - sprawność zespołu pompowego (pompa + silnik)
t - obliczeniowy czas pracy układu
Koszt całkowity
Całkowite koszty transportu cieczy, możemy określić, jako sumę kosztów inwestycyjnych Ki i kosztów eksploatacji Ke, wzór (14).
K = K_i + K_e (14)
Metody wyznaczania kosztów inwestycyjnych i zdyskontowanych kosztów eksploatacyjnych omówiono na stronie Obliczenia – optymalna średnica rurociągu.
Przebieg krzywej kosztów inwestycyjnych i kosztów energii pokazany jest na rys. 5.
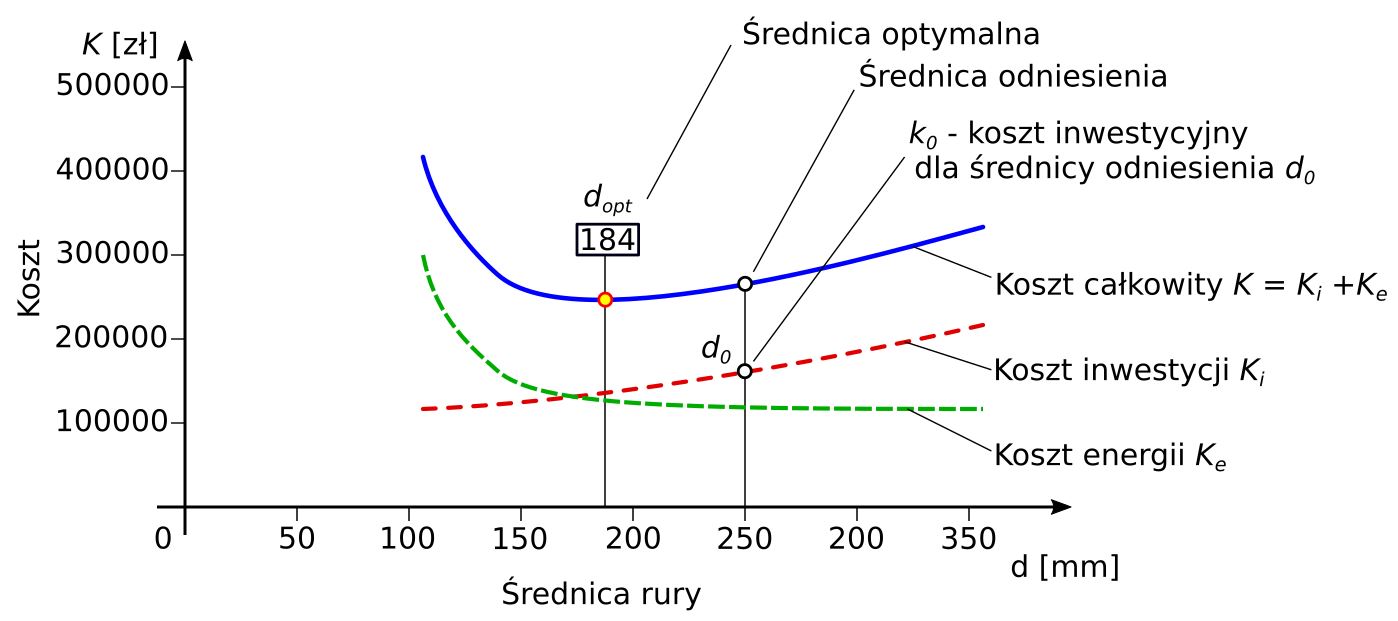
Rys. 5. Funkcja kosztów transportu rurowego
Analityczne wyznaczanie średnicy optymalnej
Do wzoru (14) podstawiamy wzory na koszty: inwestycyjne (7) oraz energii (14), (13), (12) i (11). Na tej podstawie otrzymamy wyrażenie na całkowity koszt transportu w postaci (15).
K = L \cdot k_s + L \cdot {k_0 \over d_0^2} \cdot d_{opt}^2 + {Q \cdot H_g \cdot \rho \cdot g \cdot t \cdot k_j \over \eta} + {8 \cdot \lambda \cdot \rho \cdot L \cdot Q^3 \cdot t \cdot k_j \over \eta \cdot \pi^2 \cdot d_{opt}^5} (15)
Optymalna średnica rurociągu będzie się pokrywała z minimum funkcji kosztów. Położenie tego punku możemy obliczyć przez przyrównanie pochodnej funkcji kosztów po średnicy do zera.
{dK\over dd} = 0 (16)
Po obliczeniu pochodnej wzoru (16) otrzymamy wyrażenie (17) na minimum kosztów.
{dK \over dd} = 2 \cdot L \cdot {k_0 \over d_0^2} \cdot d_{opt} - 5 \cdot {8 \cdot \lambda \cdot \rho \cdot L \cdot Q^3 \cdot t \cdot k_j \over \eta \cdot \pi^2 \cdot d_{opt}^6 } = 0 (17)
Po uporządkowaniu pochodnej (17) otrzymamy wyrażenia (18) i (19).
{k_0 \over d_0^2} \cdot d_{opt} = {20 \cdot \lambda \cdot \rho \cdot Q^3 \cdot t \cdot k_j \over \eta \cdot \pi^2 \cdot d_{opt}^6} (18)
d_{opt}^7 = {20 \cdot \lambda \cdot \rho \cdot Q^3 \cdot t \over \eta \cdot \pi^2} \cdot d_0^2 \cdot {k_j \over k_0} (19)
Ostatecznie wyrażenie na optymalną średnicę rurociągu przybiera postać (20).
d_{opt} = \sqrt [7] {{20 \cdot \lambda \cdot \rho \cdot Q^3 \cdot t \over \eta \cdot \pi^2} \cdot d_0^2 \cdot {k_j \over k_0}} (20)
Jak wynika ze wzoru (20), optymalna średnica rurociągu nie zależy od: geometrycznej wysokości podnoszenia H, kosztów stałych Ks i długości rurociągu L.
PAMIĘTAJ !
- Przy dokładnym wyznaczaniu średnicy rurociągu koszty eksploatacyjne powinny być zdyskontowane.
Warto sprawdzić
