Interpolacja charakterystyk pompy krzywą 2-go stopnia

Na podstawie jednowymiarowej teorii pomp  można wywieźć, że charakterystyki teoretyczne pompy są liniami prostymi.

Uwzględniając fakt, że straty przepływu (także w pompie) zmieniają się z kwadratem prędkości, można założyć, że „teoretycznie” charakterystyka przepływu pompy H(Q) będzie wielomianem 2-go stopnia.

We współrzędnych H–Q moc hydrauliczna pompy jest opisana liniową charakterystyką teoretyczną, co oznacza, że we współrzędnych P–Q charakterystyka mocy jest parabolą. Uwzględniając fakt, że straty mechaniczne, w tym straty tarcia tarcz wirujących, nie zależą od wydajności, można założyć, że „teoretycznie” charakterystyka mocy pompy P(Q) będzie wielomianem 2-go stopnia.

W pompach występuje wiele zjawisk nie poddających się opisowi teorii jednowymiarowej maszyn przepływowych i stosowanie wielomianu 2-go stopnia (modelu kwadratowego) do opisu charakterystyk energetycznych pompy w całym zakresie wydajności czasem prowadzi do znacznych błędów.

Jednak w wielu praktycznych przypadkach analizę pomp i układów możemy zawęzić do okolic punktu pracy lub punktu BEP. Wówczas model kwadratowy i możliwość opisu charakterystyk w postaci funkcji jest bardzo przydatna.

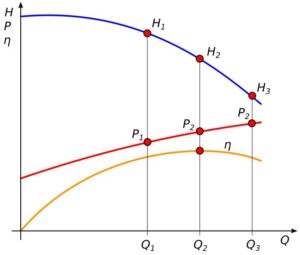
Rys.1. Interpolacja charakterystyk energetycznych na podstawie trzech punktów

Funkcję przepływu i mocy pompy w postaci wielmianów 2-go stopnia przedstawiają wzory 1 i 2.

H=A0+A1⋅Q+A2⋅Q2H = A_0 + A_1 \cdot Q + A_2 \cdot Q^2  (1)

P=B0+B1⋅Q+B2⋅Q2P = B_0 + B_1 \cdot Q + B_2 \cdot Q^2  (2)

Q - wydajność
H - wysokość podnoszenia
P - moc
ρ - gęstość
g - przyśpieszenie ziemskie
A0, A1, A2 - współczynniki równania charakterystyki przepływu
B0, B1, B2 - współczynniki równania charakterystyki mocy

Sposób wyznaczania współczynników równania na podstawie trzech wybranych punktów charakterystyki przepływu przedstawiono poniżej.

Układ równań dla punktów 1, 2 i 3.

H1=A0+A1⋅Q1+A2⋅Q12H_1 = A_0 + A_1 \cdot Q_1 + A_2 \cdot Q_1^2  (3)

H2=A0+A1⋅Q2+A2⋅Q22H_2 = A_0 + A_1 \cdot Q_2 + A_2 \cdot Q_2^2  (4)

H3=A0+A1⋅Q3+A2⋅Q32H_3 = A_0 + A_1 \cdot Q_3 + A_2 \cdot Q_3^2  (5)

Po odjęciu stronami równa 4 i 3 oraz 5 i 4 otrzymamy dwa niezależne równania baz współczynnika A0.

H2−H1=A1⋅(Q2−Q1)+A2⋅(Q22−Q12)H_2 - H_1 = A_1 \cdot \left (Q_2 - Q_1 \right ) + A_2 \cdot \left ( Q_2^2 - Q_1^2 \right )  (6)

H3−H2=A1⋅(Q3−Q2)+A2⋅(Q32−Q22)H_3 - H_2 = A_1 \cdot \left (Q_3 - Q_2 \right ) + A_2 \cdot \left ( Q_3^2 - Q_2^2 \right )  (7)

Porządkujemy równania 6 i 7 tak aby współczynnik A1 był po tej samej stronie.

A1⋅(Q2−Q1)=H2−H1−A2⋅(Q22−Q12)A_1 \cdot \left (Q_2 - Q_1 \right ) = H_2 - H_1 - A_2 \cdot \left ( Q_2^2 - Q_1^2 \right )  (8)

A1⋅(Q3−Q2)=H3−H2−A2⋅(Q32−Q22)A_1 \cdot \left (Q_3 - Q_2 \right ) = H_3 - H_2 - A_2 \cdot \left ( Q_3^2 - Q_2^2 \right )  (9)

Eliminujemy współczynnik A1 przez podzielenie stronami równania 8 przez 9.

Q2−Q1Q3−Q2=H2−H1−A2⋅(Q22−Q12)H3−H2−A2⋅(Q32−Q22){Q_2 - Q_1 \over Q_3 - Q_2} = {{H_2 - H_1 - A_2 \cdot \left ( Q_2^2 - Q_1^2 \right )} \over {H_3 - H_2 - A_2 \cdot \left ( Q_3^2 - Q_2^2 \right )}}  (10)

W celu wyeliminowania ułamków mnożymy równanie 10 przez mianowniki obu stron.

(H3−H2)⋅(Q2−Q1)−A2⋅(Q32−Q22)⋅(Q2−Q1)=\left ( H_3 - H_2 \right ) \cdot \left ( Q_2 - Q_1 \right ) - A_2 \cdot \left ( Q_3^2 - Q_2^2 \right ) \cdot \left ( Q_2 - Q_1 \right ) =

(H2−H1)⋅(Q3−Q2)−A2⋅(Q22−Q12)⋅(Q3−Q2) \left ( H_2 - H_1 \right ) \cdot \left ( Q_3 - Q_2 \right ) - A_2 \cdot \left ( Q_2^2 - Q_1^2 \right ) \cdot \left ( Q_3 - Q_2 \right )  (11)

Po uporządkowaniu równania 11 uzyskujemy wyrażenie na współczynnik A2 .

A2=(H2−H1)⋅(Q3−Q2)−(H3−H2)⋅(Q2−Q1)(Q22−Q12)⋅(Q3−Q2)−(Q32−Q22)⋅(Q2−Q1) A_2 = {{\left ( H_2 - H_1 \right ) \cdot \left ( Q_3 - Q_2 \right ) - \left ( H_3 - H_2 \right ) \cdot \left ( Q_2 - Q_1 \right )} \over {\left ( Q_2^2 - Q_1^2 \right ) \cdot \left ( Q_3 - Q_2 \right ) - \left ( Q_3^2 - Q_2^2 \right ) \cdot \left ( Q_2 - Q_1 \right )}}  (12)

Na podstawie równania 6 wyznaczamy współczynnik A1.

A1=H2−H1−A2⋅(Q22−Q12)Q2−Q1A_1= {{H_2 - H_1 - A_2 \cdot \left ( Q_2^2 - Q_1^2 \right )} \over Q_2 - Q_1}  (13)

Współczynnik A0 wyznaczamy na podstawie równania 2.

A0=H1−A1⋅Q1−A2⋅Q12A_0 = H_1 - A_1 \cdot Q_1 - A_2 \cdot Q_1^2  (14)

W ten sam sposób postępujemy także dla charakterystyki mocy.

Wzór na sprawność pompy ma postać:

η=Q⋅H⋅ρ⋅gP\eta = { Q \cdot H \cdot \rho \cdot g \over P}  (15)

Na podstawie równań 1, 2 i 15 równanie charakterystyki sprawności będzie miało postać:

η=Q⋅(A0+A1⋅Q+A2⋅Q2)⋅ρ⋅gB0+B1⋅Q+B2⋅Q2\eta = { Q \cdot \left ( A_0 + A_1 \cdot Q + A_2 \cdot Q^2 \right ) \cdot \rho \cdot g \over B_0 + B_1 \cdot Q + B_2 \cdot Q^2}  (16)

PAMIĘTAJ

  • Charakterystyka przepływu i mocy są zbliżone do paraboli (krzywej 2-go stopnia)
  • Do wyznaczenia współczynników równań 1 i 2 można wykorzystać także metodę aproksymacji na podstawie większej liczby punktów
  • Przy wykorzystaniu metod aproksymacyjnych, funkcja (szczególnie wyższych rzędów) „ucieka” od punktów na końcach przedziałów
  • Do opisu charakterystyk w całym zakresie lepiej stosować funkcje sklejane lub funkcje Beziera

WARTO SPRAWDZIĆ: