REZYSTANCJA RUROCIĄGU
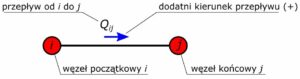
Rys. 1. Graf pojedynczego rurociągu
Straty przepływu przez pojedynczy rurociąg, między węzłami ij, opisujemy jako sumę strat liniowych i miejscowych.
h_{ij} = h_{l \ ij} + h_{m \ ij} (1)
Więcej o obliczeniach strat liniowych h_{l \ ij}
Więcej o obliczeniach strat miejscowych h_{l \ ij}
Po podstawieniu zależności na straty liniowe i miejscowe otrzymamy:
h_{ij} = {\lambda \cdot {l \over d}} \cdot {v^2 \over 2 \cdot g}+\zeta \cdot {v^2 \over 2 \cdot g} = {\lambda \cdot {l \over d}} \cdot {1 \over 2 \cdot g \cdot A^2}\cdot Q^2+\Sigma \zeta \cdot {1 \over 2 \cdot g \cdot A^2}\cdot Q^2 (2)
W obliczeniach przepływów turbulentnych możemy przyjąć, że straty zmieniają się z kwadratem prędkości. Ponieważ średnica rury d nie zmienia się – nie zmienia się także pole jej przekroju A – więc przepływ przez rurę Q jest proporcjonalny do średniej prędkości v.
Q = v \cdot A (3)
Wprowadzając przyjęte uproszczenia wzór na straty przepływu przez pojedynczy rurociąg możemy zapisać jako sumę iloczynów rezystancji liniowej r i rezystancji miejscowej m przez kwadrat przepływu:
h_{ij} = r \cdot Q^2+m \cdot Q^2 (4)
Ostatecznie, rezystancja rurociągu R definiujemy jako sumą rezystancji liniowej i miejscowej.
h_{ij} = (r + m) \cdot Q^2 = R \cdot Q^2 (5)
Tak więc rezystancja rurociągu R opisuje wszystkie straty rurociągu w kwadratowym modelu przepływu.
hl – straty liniowe hm – straty miejscowe v - średnia prędkość przepływu Q - przepływu r - rezystancja liniowa m – rezystancja miejscowa R – rezystancja rurociągu
PAMIĘTAJ !
- Model „kwadratowy” dobrze się sprawdza w przypadku większości obliczeń dla wody. Należy rozważyć zastosowanie innego modelu, gdy mamy do czynienia z cieczą o większej lepkości i małą prędkością przepływu.
Warto sprawdzić:
- Charakterystyka układu otwartego
- Pomiar charakterystyki układu
- Norma PN-76/M-34034 – Zasady obliczeń strat ciśnienia
