Zagadnienie uderzenia hydraulicznego przedstawię poprzez prostą analogię kolejowo-hydrauliczną. Załóżmy, że wagon jest odpowiednikiem elementu cieczy, a jego masa jest równa masie elementu cieczy. Sprężystość elementu jest reprezentowana przez połączenia sprężyste wagonów, a opory przepływu przez siły tarcia. Pociąg napędza lokomotywa (pompa), umieszczona na początku składu. Jeśli pociąg porusza się ze stałą prędkością, to układ będzie w równowadze i siły sprężystości zrównoważą siły tarcia. W momencie nagłego zatrzymania pociągu, co w rurociągu odpowiada awaryjnemu wyłączeniu pompy, między wagonami wystąpią siły, które doprowadzą do jego zatrzymania. Siły te mają charakter fali gasnącej, przebiegającej wzdłuż pociągu.
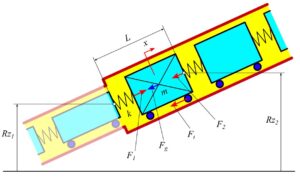
Rys.1. Siły działające na wybrany element cieczy
Wybierzmy dowolny element cieczy. Początek elementu oznaczmy indeksem 1, a koniec indeksem 2. Przyjmijmy kierunek dodatni od 1 do 2.
Równanie ruchu elementu opisuje II zasada dynamiki, wzór 1 .
m \cdot {d^2x \over dt^2} = \Sigma F (1)
L - długość elementu m - masa elementu x - przemieszczenie elementu ΣF - suma sił działających na element t - czas d2x/dt2 - przyspieszenie
Zakładam, że element cieczy jest mały.
Na element działają siły:
- naporu sprężyny na początek elementu F1
- naporu sprężyny na koniec elementu F2
- składowa ciężaru elementu Fg
- tarcia o ścianki rurociągu Ft
Siły te równoważone są siłą bezwładności elementu. Równowagę sił działających na element przedstawia wzór 2.
m {d^2x \over dt^2} = F_1 - F_2 - F_t - F_g (2)
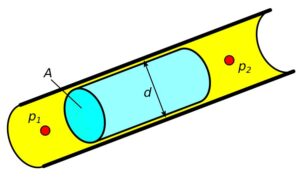
Rys.2. Ciśnienia działające na wybrany element cieczy
Jeżeli do opisu stany dynamicznego elementu wykorzystamy pole jego przekroju, to równanie 2 możemy przekształcić do postaci 3.
L \cdot A \cdot \rho \cdot {d^2x \over dt^2} = A \cdot ( p_1 - p_2 - p_t - p_g ) (3)
d - średnica elementu (średnica wewnętrzna rurociągu) A - pole przekroju elementu p1 - ciśnienie przed elementem p2 - ciśnienie za elementem pg - ciśnienie wywołane ciężarem elementu pt - ciśnienie strat hydraulicznych (tarcia) ρ - gęstość cieczy
Zmianę objętości przetłoczonej cieczy w czasie opisują równania 4 i 5.
dV = A \cdot dx (4)
{dV \over dt} = Q (5)
Po podstawieniu równania 4 i 5 do 3 otrzymamy równanie ruchu elementu cieczy w postaci 6.
{dQ \over dt} = {A \over L \cdot \rho} \cdot \left ( p_1 - p_2 - p_t - p_g \right ) (6)
dV - zmiana objętości Q - przepływ
Ciśnienie na końcach elementów p1 i p2 jest skutkiem wzajemnego sprężystego oddziaływania sąsiadujących elementów cieczy.
Sprężysta zmiana średnicy rurociągu i wynikająca z niej zmiana objętości elementu cieczy, opisana jest wzorem 7.
\Delta V_r = V_0 \cdot {d \over E_r \cdot e} \cdot p_1 (7)
Zmiana objętości elementu, spowodowana ściśliwością cieczy, opisana jest wzorem 8.
\Delta V_c = V_0 \cdot {1 \over E_c} \cdot p_1 (8)
Całkowita zmiana objętości elementu opisana jest wzorem 9.
\Delta V = \Delta V_r + \Delta V_c = V_0 \cdot \left ( {d \over E_r \cdot e} + {1 \over E_c} \right ) \cdot p_1 (9)
Stałą, po prawej stronie równania, możemy określić jako współczynnik sprężystości objętościowej elementu i oznaczyć ko, wzór 10.
k_o = V_0 \cdot \left ( {d \over E_r \cdot e} + {1 \over E_c} \right ) (10)
\Delta V = k_o \cdot p_1 (11)
Ostatecznie ciśnienie przed segmentem określa wzór 12.
p_1 = {1 \over k_o} \cdot \Delta V (12)
V0 - objętość początkowa elementu ΔVr - zmiana objętości elementu spowodowana sprężystością rurociągu ΔVc - zmiana objętości elementu spowodowana ściśliwością cieczy Er - moduł sprężystości materiału rurociągu Ec - moduł sprężystości cieczy e - grubość ścianki rurociągu ko - współczynnik sprężystości objętościowej elementu
Ciśnienie wywołane ciężarem elementu pg obliczamy z równania 13.
p_g = \left (Rz_2 - Rz_1 \right ) \cdot \rho \cdot g (13)
Ciśnienie strat hydraulicznych elementu obliczamy na podstawie wzoru Darcy-Weisbacha i wzoru na straty miejscowe 14.
h_t = \left( {\lambda \cdot {L \over d} + \zeta} \right) \cdot {v^2 \over 2 \cdot g} (14)
Przepływ i średnia prędkości w rurociągu związane są zależnością 15.
v = {Q \over A} = {4 \cdot Q \over \pi \cdot d^2} (15)
Po podstawieniu zależności 15 do 14 otrzymamy wzór 16 na ciśnienie strat tarcia.
p_t = \rho \cdot g \left( {\lambda \cdot {L \over d} + \zeta} \right) \cdot {1 \over 2 \cdot g} \cdot {16 \over \pi^2 \cdot d^4} \cdot Q^2 (16)
Po uporządkowaniu, wzór na ciśnienie, wywołane tarciem przyjmuje postać 17.
p_t = {8 \cdot \rho \over \pi^2 \cdot d^4} \left( {\lambda \cdot {L \over d} + \zeta} \right) \cdot Q^2 (17)
Współczynnik przed Q2 ma wartość stałą dla wybranego elementu, więc możemy wzór 17 zapisać w postaci prostej zależności kwadratowej 18.
p_t = R_p \cdot Q^2 (18)
Aby uwzględnić zmiany kierunku działania sił tarcia, należy zachować zwrot siły, jak to pokazano we wzorze 19.
p_t = R_p \cdot abs(Q) \cdot Q (19)
Rz1 - rzędna początku elementu cieczy Rz2 - rzędna końca elementu cieczy v - prędkość elementu cieczy λ - współczynnik strat liniowych ζ- współczynnik strat miejscowych Rp - rezystancja elementu cieczy
Ciśnienie w rurociągu nie może spaść poniżej ciśnienia prężności par cieczy pv. Jeżeli założymy, że na zewnątrz rurociągu panuje ciśnienie atmosferyczne pb, to minimalne ciśnienie w rurociągu określa wzór 20.
p_{min} = p_v - p_b (20)
PAMIĘTAJ
- Opis uderzenia hydraulicznego, za pomocą analogii kolejowej, nie jest dokładny
- W wielu przypadkach analogia kolejowa jest wystarczającym sposobem analizy uderzenia, w rzeczywistych układach pompowych
- Wielkość elementu cieczy wpływa na dokładność obliczeń
- Obliczenia odkształcenia sprężystego rurociągu i ściśliwości cieczy są odniesione do początku elementu, co zwykle nie prowadzi do nadmiernych błędów
- W obliczeniach posługujemy się ciśnieniem względnym (względem pb), stąd ciśnienie minimalne może mieć wartość ujemną
Warto sprawdzić:
