Przyśpieszenie cieczy w układzie – Pumps and Pumping System

PRZYŚPIESZENIE CIECZY W UKŁADZIE

Równowagę dynamiczną cieczy w układzie pompowym można opisać prostym modelem pokazanym na rys. 1.

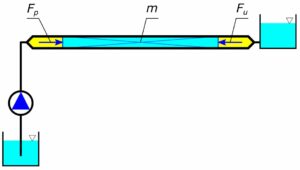
Rys. 1. Model dynamiczny układu pompowego

W prostych obliczeniach masę cieczy w całym układzie możemy skupić w jednym punkcie i opisać stałą m.

Na podstawie równania ruchu postępowego, przyśpieszenie cieczy możemy zapisać równaniem:

$a = {1 \over m} (F_p - F_u)$

a - przyśpieszenie cieczy [m/s2]
m - masa cieczy w rurociągu [kg]
Fp - siła parcia pompy [N]
Fu - siła oporów układu [N]

Masę cieczy w układzie można obliczyć na podstawie objętości:

$m = A \cdot L \cdot \rho$

Siłę parcia można wyznaczyć na podstawie wysokości podnoszenia pompy:

$F_p = A \cdot H_p \cdot \rho \cdot g$

Siłę oporów można wyznaczyć na podstawie charakterystyki układu:

$F_u = A \cdot (H_{st} + R \cdot Q^2) \cdot \rho \cdot g$

Po podstawieniu wyrażeń na masę i siły do równania ruchu, otrzymamy:

$a = {g \over L}(H_p - H_u) = {g \over L}(H - H_{st} - R \cdot Q^2)$

a - przyśpieszenie cieczy [m/s2]
g - przyśpieszenie ziemskie [m/s2]
L - długość rurociągu [m]
Hp - wysokość podnoszenia pompy [m]
Hu - wysokość podnoszenia układu [m]
Hst - statyczna wysokość podnoszenia układu [m]
R - rezystancja rurociągu [s2/m5]
Q - przepływ [m3/s]

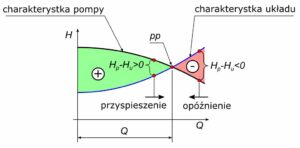
Rys. 2. Przyspieszenie cieczy w układzie

PAMIĘTAJ ! Czynniki wpływające na przyśpieszenie cieczy w układzie:

Im dłuższy rurociąg, tym przyśpieszenie cieczy jest mniejsze
Im większa nadwyżka wysokość podnoszenia pompy H_p nad charakterystyką układu H_u, tym przyśpieszenie większe.
Jeżeli wysokość podnoszenia pompy H_p będzie większa niż charakterystyka układu H_p>H_u – ciecz przyśpieszy do punktu pracy – punktu równowagi.
Jeżeli wysokość podnoszenia pompy H_p będzie mniejsza niż charakterystyka układu H_p<H_u – ciecz zwolni do punktu pracy – punktu równowagi.

Warto sprawdzić: