Charakterystyka przepływu i mocy pompy może być opisana wielomianem 2-go stopnia, równania 1 i 2.
H = A_0 + A_1 \cdot Q + A_2 \cdot Q^2 (1)
P = B_0 + B_1 \cdot Q + B_2 \cdot Q^2 (2)
W analizach pracy pomp regulowanych prędkością obrotową przydatne jest przeliczenie współczynników funkcji charakterystyk na inną prędkość. Zmianę prędkości wygodnie jest w tym przypadku opisać względną zmianą prędkości r, wzór 3.
r={n \over n_0} (3)
Q - wydajność H - wysokość podnoszenia P - moc ρ - gęstość g - przyśpieszenie ziemskie A0, A1, A2 - współczynniki równania charakterystyki przepływu B0, B1, B2 - współczynniki równania charakterystyki mocy n - prędkość obrotowa n0 - nominalna prędkość obrotowa r - względna prędkość obrotowa
Zgodnie z teorią podobieństwa maszyn wirowych przeliczenie punktów charakterystyki odbywa się na podstawie zależności 4, 5 i 6.
Q \sim r (4)
H \sim r^2 (5)
P \sim \rho \cdot r^3 (6)
Wartości funkcji wysokości podnoszenia H, zgodnie ze wzorem 5, są proporcjonalne do r2 a argumenty Q, zgodnie ze wzorem 4, odwrotnie proporcjonalnie do r.
H = \left ( A_0 + A_1 \cdot {Q \over r} + A_2 \cdot \left ( Q \over r \right )^2 \right ) \cdot r^2 (7)
Po uporządkowaniu otrzymujemy równanie 8 – funkcję przepływu dla dowolnej prędkości względnej.
H = A_0 \cdot r^2 + A_1 \cdot r \cdot Q + A_2 \cdot Q^2 (8)
W ten sam sposób postępujemy dla równania charakterystyki mocy.
P = \left ( B_0 + B_1 \cdot {Q \over r} + B_2 \cdot \left ( Q \over r \right )^2 \right ) \cdot r^3 (9)
P = B_0 \cdot r^3 + B_1 \cdot r^2 \cdot Q + B_2 \cdot r \cdot Q^2 (10)
Przykład
Podstawowe charakterystyki przepływu i mocy pompy określone są za pomocą trzech punktów.
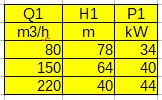
Rys.1. Punkty charakterystyk pompy dla n=3000 obr/min
Pozostałe parametry pompy.
- Prędkość obrotowa n = 2500 obr/min
- Nominalna prędkość obrotowa n0 = 3000 obr/min
- Gęstość cieczy ρ = 1000 kg/m3
Na podstawie wzoru 3 wyznaczamy prędkość względną r.
r={n \over n_0}= {2500/3000} = 0,8333
Współczynniki równań 1 i 2 obliczamy na podstawie wzorów opisanych na stronie Interpolacja charakterystyk pompy krzywą 2-go stopnia.
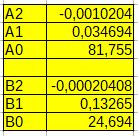
Rys.2. Współczynniki równań interpolacyjnych dla n=3000 obr/min
Sprawność pompy obliczamy ze wzoru:
\eta = {Q \cdot H \cdot \rho \cdot g \over P}
Podstawowe charakterystyki: przepływu, mocy i sprawności pompy obliczanie na podstawie równań 1 i 2 pokazano na rys. 3 i 4.
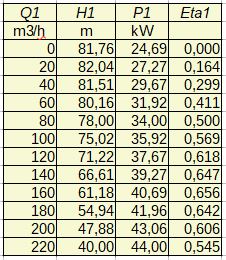
Rys.3. Punkty charakterystyk pompy dla n=3000 obr/min
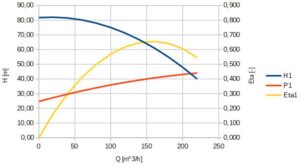
Rys.4. Charakterystyk pompy dla n=3000 obr/min
Współczynniki równań charakterystyk, dla r=0,833 (n=2500) obliczamy na podstawie wzorów 8 i 10.
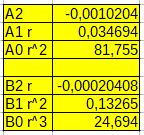
Rys.5. Współczynniki równań interpolacyjnych dla n=2500 obr/min
Charakterystyki: przepływu, mocy i sprawności pompy przy n=2500 obliczanie na podstawie wzorów 8 i 10 pokazano na rys. 6 i 7.
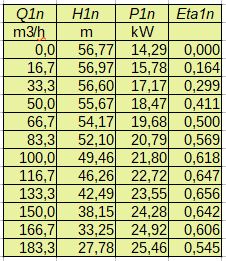
Rys.6. Punkty charakterystyk pompy dla n=2500 obr/min
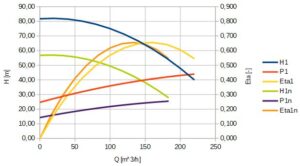
Rys.7. Charakterystyk pompy dla n=3000 i 2500 obr/min
Arkusz kalkulacyjny: PrzeliczanieFunkcjiCharakterystyk.ods
Arkusz kalkulacyjny: PrzeliczanieFunkcjiCharakterystyk.xlsx
PAMIĘTAJ
- Oznaczenia Q, H i P we wzorach 1 i 2 oznaczają wartości pierwotne
- Oznaczenia Q, H i P we wzorach 8 i 10 oznaczają wartości przeliczone
- Ekstrapolacja charakterystyk „w prawo”, dla większych wydajności jest dopuszczalna.
- Ekstrapolacja charakterystyk „w lewo – do zera”, zwykle jest dopuszczalna, jednak dla pomp o wyższych wyróżnikach szybkobieżności może prowadzić do błędów.
- Ekstrapolacja charakterystyk „w lewo – dla ujemnych wydajności”, na pewno będzie prowadzić do błędów.
WARTO SPRAWDZIĆ:
