Jako kryterium optymalnej pracy równoległej dwóch pomp regulowanych prędkością obrotową wybieram minimum mocy elektrycznej pobieranej przez układ.
P = P_1 +P_2 = min (1)
Jako zmienną niezależną wybieram prędkość obrotową pompy pierwszej n1.
Moc układu osiąga minimum wówczas gdy pochodna funkcji mocy wynosi zero.
{dP \over dn_1} = {d \left(P_1 + P_2 \right) \over dn_1} = {dP_1 \over dn_1} + {dP_2 \over dn_1}= 0 (2)
Układ będzie zużywał najmniej energii wówczas gdy suma pochodnych funkcji mocy będzie równa ZERO.
Jak wyznaczyć optymalne prędkości obrotowe pomp pokażę na przykładzie.
Rozważymy współpracę z układem dwóch różnych pomp regulowanych prędkością obrotową.
1. Parametry
Charakterystyki pomp są określone przez trzy wartości współrzędnych w pobliżu punktu BEP.
Pompa 1
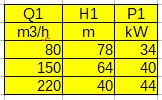
Rys.1. Punkty charakterystyk pompy 1 dla n1=3000 obr/min
Pompa 2
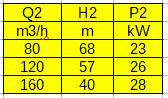
Rys.2. Punkty charakterystyk pompy 1 dla n2=3000 obr/min
Przebieg charakterystyki układu określają parametry:
- Qw = 300 m3/h – wymagana wydajność
- Hw = 40 m – wymagana wysokość podnoszenie
- H0 = 20 m – geometryczna wysokość podnoszenia
Q1, Q2 - wydajność H1, H2 - wysokość podnoszenia P1, P2 - moc Qw - wymagana wydajność układu Hw - wymagana wysokość podnoszenia H0 - geometryczna wysokość podnoszenia
2. Interpolacja charakterystyk
Na podstawie trzech punktów przebieg charakterystyk przepływu i mocy pomp opisujemy wielomianami 2-go stopnia.
H = A_0 + A_1 \cdot Q + A_2 \cdot Q^2 (3)
P = B_0 + B_1 \cdot Q + B_2 \cdot Q^2 (4)
Współczynniki równań pokazano na rys. 3 i 4.
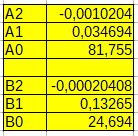
Rys. 3. Współczynniki równań charakterystyk pompy 1
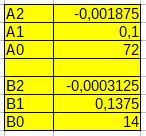
Rys. 4. Współczynniki równań charakterystyk pompy 2
Przebieg charakterystyk pomp pokazano na rys. 5 i 6.
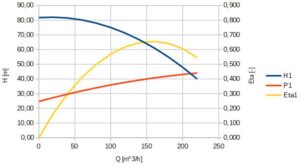
Rys. 5. Charakterystyki pompy 1 dla n1=3000 obr/min
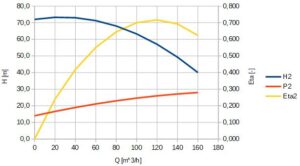
Rys. 6. Charakterystyki pompy 2 dla n2=3000 obr/min
Sprawność pompy obliczono ze wzoru 5.
\eta = {Q \cdot H \cdot \rho \cdot g \over P} (5)
Równanie charakterystyki układu określa wzór 6.
H_u = H_0 + R \cdot Q^2 = H_0 + {H_w - H_0 \over Q_w^2} \cdot Q^2 (6)
A0, A1, A2 - współczynniki równania charakterystyki przepływu B0, B1, B2 - współczynniki równania charakterystyki mocy ρ - gęstość g - przyśpieszenie ziemskie R - rezystancja rurociągu
3. Współpraca równoległa pomp
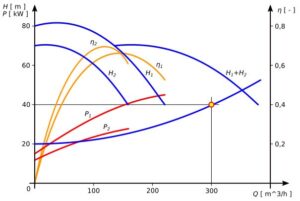
Rys.7. Suma równoległa charakterystyk pomp P1 i P2 dla n=3000 obr/min
Jak wynika z rys. 7 wydajność sumy równoległej dwóch pomp jest większa od zapotrzebowania układu, co oznacza, że jedna lub obie pompy powinny być regulowane prędkością obrotową.
Z analizy współpracy pomp można wywieźć zależności 7 i 8.
Wymaganą wydajność układu Qw jest sumą wydajności pompy P1 i P2.
Q_w = Q_1 + Q_2 (7)
Wysokość podnoszenia obu pomp jest taka sama.
H_w = H_1 = H_2 (8)
Pytanie brzmi: jaką prędkość obrotową powinna mieć pompa 1 i jaką prędkość pompa 2.
4. Charakterystyki pomp dla dowolnej prędkości obrotowej
Względna prędkość obrotowa r, określona jest wzorem 9.
r={n \over n_0} (9)
Zgodnie z teorią podobieństwa maszyn wirowych charakterystyki energetyczne ze zmianą prędkości obrotowej opisane są wzorami 10 i 11.
H = A_0 \cdot r^2 + A_1 \cdot r \cdot Q + A_2 \cdot Q^2 (10)
P = B_0 \cdot r^3 + B_1 \cdot r^2 \cdot Q + B_2 \cdot r \cdot Q^2 (11)
n - prędkość obrotowa n0 - nominalna prędkość obrotowa r - względna prędkość obrotowa
4. Optymalizacja współpracy pomp
Krok 1. Wyznaczenie funkcję wydajności pompy Q1 w zależności od prędkości r1 przy stałej wysokości podnoszenia H=const.
Q_1 = f(r_1, H=const) (12)
Przekształcamy równanie 10 do postaci równania kwadratowego względem Q1.
A_{2.1} \cdot Q_1^2 + A_{1.1} \cdot r_1 \cdot Q_1 + A_{0.1} \cdot r_1^2 - H = 0 (13)
Rozwiązaniem równania jest zależność 14 .
Q_1 = {- A_{1.1} \cdot r_1 - \sqrt{A_{1.1}^2 \cdot r_1^2 - 4 \cdot A_{2.1} \cdot (A_{0.1} \cdot r_1^2 - H) } \over 2 \cdot A_{2.1}} (14)
Krok 2. Wyznaczenie funkcję mocy pompy P1 w zależności od prędkości r1 i wydajności Q1.
P_1 = f(n_1, Q_1, H=const) (15)
Funkcję mocy pompy uzyskamy przez podstawie do równania 11 wartości z zależności 14.
P_1 = B_{0.1} \cdot r_1^3 + B_{1.1} \cdot r_1^2 \cdot Q_1 + B_{2.1} \cdot r_1 \cdot Q_1^2 (16)
Dla współczynników charakterystyk pompy 1 z rys. 3 przebieg wydajności Q1 i mocy P1 w zależności od prędkości względnej r1 i prędkości obrotowej n1 pokazano na rys.8.

Rys.8. Funkcja wydajności i mocy pompy 1 w zależności od prędkości obrotowej
Krok 3. Wyznaczenie funkcji wydajności pompy 2 w zależności od prędkości obrotowej pompy 1 przy stałej wysokości podnoszenia na podstawie równania 7.
Q_2 = Q_w - Q_1 (17)
Krok 4. Wyznaczenie funkcji prędkości obrotowej r2 z zależności od wydajności pompy 2 a w konsekwencji od r1, przy stałej wysokości podnoszenia.
r_2 = f(Q_2, H=const) (18)
Do wzoru 10 podstawiamy zależności ze wzorów 17 i 14. Po uporządkowaniu uzyskamy zależność w postaci równania kwadratowego 19.
A_{0.2} \cdot r_2^2 + A_{1.2} \cdot Q_2 \cdot r_2 + A_{2.2} \cdot Q_2^2 - H = 0 (19)
Ostateczne wartość względnej prędkości obrotowej określa równanie 20.
r_2 = {- A_{1.2} \cdot Q_2 - \sqrt{A_{1.2}^2 \cdot Q_2^2 - 4 \cdot A_{0.2} \cdot (A_{2.2} \cdot Q_2^2 - H) } \over 2 \cdot A_{0.2}} (20)
Krok 5. Wyznaczenie funkcji mocy pompy P2 w zależności od prędkości r1 dla określonej wartości Q2.
P_2 = f(r_2, Q_2, H=const) (21)
Funkcję mocy pompy 2 uzyskamy przez podstawie do równania 11 wartości z zależności 17 i 20.
P_2 = B_{0.2} \cdot r_2^3 + B_{1.2} \cdot r_2^2 \cdot Q_2 + B_{2.2} \cdot r_2 \cdot Q_2^2 (22)
Dla współczynników charakterystyk pompy 2 z rys. 4 przebieg wydajności Q2 i mocy P2 w zależności od prędkości względnej r1 i prędkości obrotowej n1 pokazano na rys.9.

Rys.9. Funkcja wydajności i mocy pompy 1 w zależności od prędkości obrotowej
Krok 6. Wyznaczamy optymalnej wartość prędkości obrotowej n1.
Analityczne wyznaczenie minimum sumy mocy pomp na podstawie równania 2 jest uciążliwe. Znacznie prostszym sposobem jest wykorzystanie metody przeszukiwania przedziału zmienności n1 w arkuszu kalkulacyjnym w celu znalezienia minimum funkcji P1 + P2.
Wyniki przeszukiwania przedziału pokazano na rys. 10 i 11.
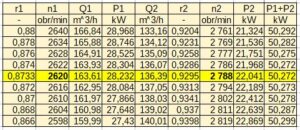
Rys.10. Przeszukiwanie przedziału zmienności r1
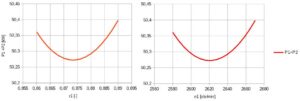
Rys.11. Minimum funkcji sumy mocy pomp P1 + P2
W pokazanym przykładzie optymalna wartość prędkości obrotowej pompy 1 wynosi n1=2620 obr/min.
Krok 7. Wyznaczenie parametrów pracy układu.
Na podstawie znanej wartości n1 możliwe jest wyznaczenie pozostałych parametrów pracy układu, jak to pokazano na rys. 10 i 12.
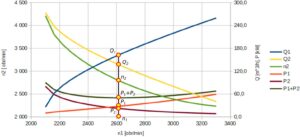
Rys.12. Optymalne parametry pracy układu
Parametry optymalne
-
- n1 = 2620 obr/min
- n2 = 2788 obr/min
- Q1 = 163,61 m3/h
- Q2 = 136,39 m3/h
- P1 = 28,23 kW
- P2 = 22,04 kW
Arkusz kalkulacyjny: Optymalne sterowanie prędkością 2 pomp.ods
Arkusz kalkulacyjny: Optymalne sterowanie prędkością 2 pomp.xlsx
PAMIĘTAJ
- Nawet nowe pompy o tym samym oznaczeniu nie są identyczne
- Pompy zmieniają swoje parametry (charakterystyki) w czasie eksploatacji
- Jeżeli współpracują ze sobą różne pompy warto poszukać optymalnych parametrów współpracy
WARTO SPRAWDZIĆ:
