Obliczenia – rozruch pompy odśrodkowej

Przyśpieszenie kątowe silnika i pompy opisuje równanie:

${d \omega \over dt}={1 \over J} \cdot \Sigma M={1 \over {J_s+J_p}} \cdot (M_s - M_p)$ (1)

dω/dt – przyśpieszenie kątowe zespołu wirującego
J – moment bezwładności zespołu wirującego
ΣM – suma momentów
J_s – moment bezwładności silnika
J_p – moment bezwładności pompy
Ms – moment silnika
Mp – moment pompy

Obliczenia symulacyjne przeprowadzę, z wykorzystaniem metod opisanych na stronie Obliczenia – całkowanie równanie ruchu cieczy , dla pompy wielostopniowej, dla dwóch skrajnych przypadków: rozruchu przy zamkniętej i otwartej zasuwie na tłoczeniu.

Rozpatrzmy przykład rozruchu pompy współpracującej z poziomym rurociągiem

W obliczeniach pominiemy zjawiska falowe.

Stałe parametry zespołu pompowego i układu
  Q_n = 400 m³/h - nominalna wydajność układu
  H_g = 0 m - geometryczna wysokość podnoszenia (układ poziomy)
  Δh_n = 630 m - straty w układzie dla nominalnej wydajności
  M₀/M_np = 0,2 - względny startowy moment mechaniczny pompy
  Q_m0/Q_n = 0,3 - względny zasięg startowego momentu mechanicznego
  P_n = 900 kW - nominalna (znamionowa) moc silnika
  n_n = 2986 obr/min - nominalna prędkość obrotowa silnika
  M_k/M_n = 2,5 - krotność momentu krytycznego silnika
  s_k = 0,05 - poślizg krytyczny
  α_M = 0,75 - współczynnik poprawkowy we wzorze Klossa
  I_n = 100 A - nominalny (znamionowy) prąd silnika
  I_max/I_n = 7,2 - krotność prądu rozruchowego
  α_I = 1,2 - współczynnik poprawkowy interpolacji prądu
  β_I = 0,65 - współczynnik poprawkowy interpolacji prądu
  γ_I = 0,12 - współczynnik poprawkowy interpolacji prądu
  J_s = 20 kg m² - moment bezwładności silnika
  J_zp/J_s = 1,46 - względny moment bezwładności zespołu / silnika
  ρ = 1000 kg/m3 - gęstość cieczy

Charakterystyki energetyczne i moment rozruchowy pompy zostały opisane na stronie Charakterystyki rozruchowe pompy.

Aproksymacja charakterystyk energetycznych pompy ze strony charakterystyki rozruchowe pompy Tab. 1

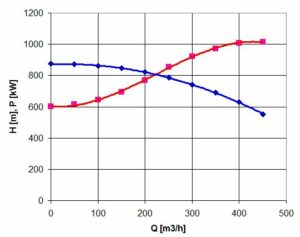
Rys.1. Punkty charakterystyki i krzywe aproksymacyjne

Uwaga
Zmienne parametry pracy pompy zostaną opisane prostymi funkcjami aproksymacyjnymi.
Aproksymacja funkcji momentu i prądu silnika prowadzi do nieakceptowalnych błędów. W tym przypadku zastosowałem również proste zmodyfikowane funkcję interpolacyjne. 
W dokładnych obliczeniach krzywe charakterystyczne pompy i silnika można dokładnie opisać funkcjami sklejanymi (funkcje Beziera, wielomiany 3-go stopnia).

Funkcję kwadratowa aproksymująca charakterystykę przepływu pompy uzyskano przez wywołanie narzędzia arkusza excell:

ustaw kursor na wykresie charakterystyki
kliknij prawym przyciskiem myszy
z menu kontekstowego wybierz <Dodaj linię trędu>
wybierz wielomian 2-go stopnia (zakładka Typ)
zaznacz opcję <wyświetl równanie na wykresie> (zakładka Opcje)
skopiuj tekst równanie i wykorzystaj go do obliczeń.

Jeżeli w równaniu współczynniki mają mniej niż 4 miejsca znaczące, zmień formatowanie wyświetlania równania.

W omawianym przykładzie równanie aproksymacyjne charakterystykę przepływu pompy ma postać:

$H=-0,0017977 \cdot Q^2+0,10643 \cdot Q+872,04$ (2)

a funkcja trzeciego stopnia aproksymująca charakterystykę mocy pompy:

$P=-0,0000121616 \cdot Q^3+0,0081879 \cdot Q^2-0,3153 \cdot Q+605,3$ (3)

Przed przystąpieniem do dalaszych obliczeń wyznaczamy stałe parametry układu:

synchroniczną prędkość kątową ω_s ze wzoru:

$\omega_s={2 \cdot \pi \cdot 3000 \over 60}=314,2 \ {1 \over s}$ (4)

nominalną prędkość kątową ω_n ze wzoru:

$\omega_n={2 \cdot \pi \cdot n_n \over 60}=312,7 \ {1 \over s}$ (5)

moment nominalny silnika

$M_n={P_n \over \omega_n}=2878 \ Nm$ (6)

oszacowany moment bezwładności zespołu pompowego

$I_{zp}=I_s \cdot {J_{zp} \over J_s}=29,2 \ kg \ m^2$ (7)

oszacowaną rezystancję silnika R_s ze wzoru:

$R_s={P_n \over I_n^2}=90 \ \Omega$ (8)

Uwaga 
Wartość Rs będzie wykorzystywana jedynie do względnej oceny ciepła wyzwalanego podczas rozruchu z zamkniętą zasuwą w stosunku do ciepła wyzwalanego przy otwartej zasuwie.

rezystancję układu R_u ze wzoru:

$R_u={\Delta h_n \over Q_n^2}=51030 \ {s \over m^2}$ (9)

Startowy moment mechaniczny pompy z zadowalającą dokładnością opisuje model paraboliczny:

$M_m={M_0 \over M_{np}} \cdot {M_{np}} \cdot (1-{n \over n_n} \cdot {Q_n \over Q_{m0}})^2 = 0,2 \cdot M_{np} \cdot (1-{n \over n_n} \cdot {1 \over 0,3})^2$ (10)

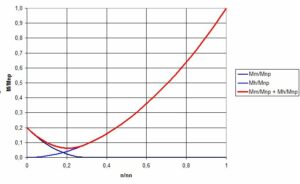
Rys.2. Względny moment rozruchowy pompy

Charakterystyka mechaniczna silnika elektrycznego została opisana na stronie Moment rozruchowy silnika.

Względny moment mechaniczny silnika, z wystarczającą dokładnością dla jakościowej oceny rozruchu, opisuje zmodyfikowane równanie Klossa:

${M \over M_n}={M_k \over M_n} \cdot {2 \cdot \alpha_M \over {{s_k \over s} + {s \over s_k}}} + 1 - \alpha_M = 2,5 \cdot {2 \cdot 0,75 \over {{0,05 \over s} + {s \over 0,05}}} +1 - 0,75$ (11)

gdzie poślizg jest zdefiniowany jako:

$s={{\omega_s - \omega} \over \omega_s} = {{314,2 - \omega} \over 314,2}$ (12)

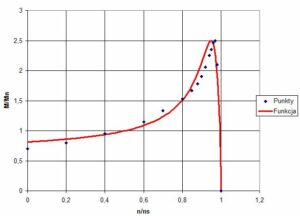
Rys.3. Względny moment rozruchowy silnika elektrycznego

Przybliżone równanie prądu silnika

${I \over I_n}={I_{max} \over I_n} \cdot \alpha - {1 \over {s^{\beta}+ \gamma}} = 7,2 \cdot 1,2 - {1 \over s^{0,65} + 0,12}$ (13)

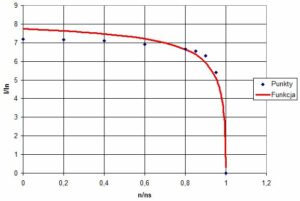
Rys.4. Względny prąd rozruchowy silnika elektrycznego

Uwaga
Do precyzyjnego opisania zmian prądu w okolicy punktu znamionowego lepiej sprawdza się liniowe przybliżenie oparte o prąd w punkcie znamionowy i zerowy prąd dla prędkości synchronicznej,

Obliczenia symulacyjne przy zamkniętej zasuwie na tłoczeniu

W tym przypadku wydajność pompy w czasie całego rozruch jest równa zero Q=0.

Rys.5. Dane silnika, pompy i układu wprowadzone do arkusza kalkulacyjnego

W obliczeniach nie wykorzystujemy ani charakterystyki przepływu pompy ani równania strat układu.

Rys.6. Algorytm obliczeń w arkuszu kalkulacyjnym

Obliczenia prowadzimy poprzez kopiowanie wierszy arkusza do dowolnego czasu symulacji liczonego w pierwszej kolumnie.

Wyniki obliczeń symulacyjnych dla zamkniętej zasuwy

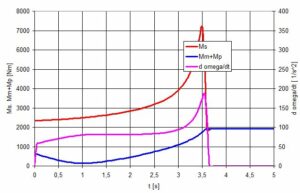
Rys.7. Moment rozruchowy silnika i pompy

W wykresu rys.7 wynika, że w układzie występuje znaczna nadwyżka momentu silnika (linia czerwona) nad momentem pompy (linia niebieska). Linie te zbiegają się po ok. 3,7s. W tym momencie stabilizuje się prędkość kątowa, patrz rys. 8.

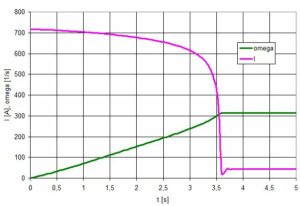
Rys.8. Prąd rozruchowy i prędkość kątowa silnika

Należy zwrócić uwagę na fakt, że prąd utrzymuje się na bardzo wysokim poziomie przez praktycznie cały czas rozruchu (ok. 3s).

Obliczenia symulacyjne przy otwartej zasuwie na tłoczeniu

W tym przypadku wysokość podnoszenia obliczona jest na podstawie charakterystyki pompy, w zależności od wydajności i prędkości kątowej H(Q,ω), a przepływ wyznaczany jest na podstawie charakterystyki układu Q=(H/R_u)^0,5.

Rys.9. Algorytm obliczeń w arkuszu kalkulacyjnym

Wyniki obliczeń symulacyjnych przy otwartej zasuwie na tłoczeniu

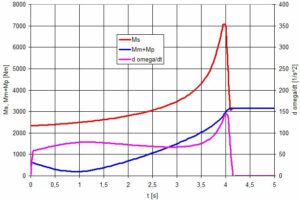
Rys.10. Moment rozruchowy silnika i pompy

Z wykresu rys.10 wynika, że nadwyżka momentu silnika (linia czerwona) nad momentem pompy (linia niebieska) w początkowej fazie rozruchu (2s) ma podobną wartość jak w czasie rozruchu przy zamkniętej zasuwie – wpływ momentu mechanicznego pompy. W końcowej fazie zaznacza się wpływ zwiększonego momentu hydraulicznego pompy. Linie momentów zbiegają się po ok. 4,2s.

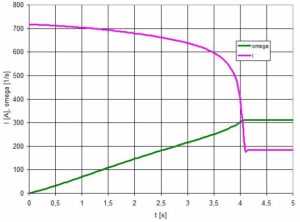
Rys.11. Prąd rozruchowy i prędkość kątowa silnika

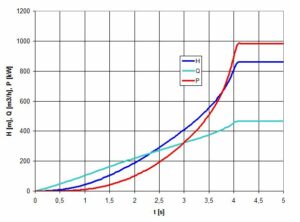
Rys.12. Wysokość ciśnienia H, przepływ Q i moc P w czasie rozruchu układu z otwartą zasuwą

Z analizy wykresów rys. 11 i 12 wynika, że wydajność pompy łagodnie rośnie, podobnie jak prędkość obrotowa, a ciśnienie i moc gwałtownie rosną w ostatniej fazie rozruchu.

Porównanie rozruchu z zamkniętą i otwartą zasuwą

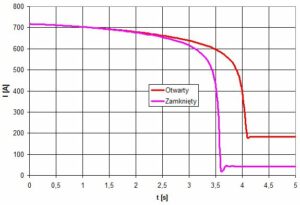
Rys.13. Porównanie zmian prądu rozruchu

Na podstawie wykresu rys.13, dla celów porównawczych możemy przyjąć, że czas rozruchu układu wynosi t_r = 4,2s. Czas rozruch przy otwartej zasuwie trwa ok 0,5s dłużej niż przy zamkniętej.

Moc cieplną rozruchu możemy oszacować na podstawie wzoru:

$P_c = R_s \cdot I^2$ (14)

Energię (ciepło) generowane podczas rozruchu (pole pod krzywą na rys.13) możemy obliczyć jako całkę mocy P_c w czasie rozruchu t_r. Z wystarczającą dokładnością wartość tej całki opisuje równanie:

$E_c = \sum\limits_{t=0}^{t=t_r} P_c \cdot dt$ (15)

Uwaga
Obliczona ilość ciepła E_c odbiega od rzeczywistej generowanej podczas rozruchu pompy i może być używane jedynie do obliczeń względnych.

W arkuszu kalkulacyjnym zapis komórek obliczających ciepło rozruchu pokazano na rys.14.

Rys.14. Oszacowanie ciepła (energii) rozruchu

Z przeprowadzonych symulacji wynika, że podczas rozruchu pompy, z zamkniętą zasuwą, prąd przepływający przez uzwojenia silnika wytwarza ciepło E_cz = 39,77 kWh, a z zasuwą otwartą E_co = 44,68 kWh.

Względny wzrost ciepła podczas rozruchu wznosi:

${E_{co} - E_{cz} \over E_{cz}} = {44,68 -37,77 \over 39,77} = 0,1234 = 12,34 \%$ (16)

Z przeprowadzonego rozważań wynika, że obciążenie cieplne silnika przy rozruchu z otwartą zasuwą wzrasta (jedynie) o 12,3%.

PAMIĘTAJ !

W obliczeniach pominięto zjawiska falowe
W obliczeniach założono, że sieć zasilająca jest sztywna (stałe napięcie)
Przyśpieszenie w ruchu obrotowym jest proporcjonalne do momentu i odwrotnie proporcjonalne do momentu bezwładności
Charakterystyki: przepływu, mocy i momentu pompy mogą być opisane wielomianami.
Charakterystyki: momentu i prądu silnika mogą być opisane funkcją Klossa i hiperbolą.
W dokładnych obliczeniach należy używać funkcji sklejanych lub funkcji Beziera (splajnów)
Możesz wykorzystać arkusz kalkulacyjny i całkowanie metodą prostokątów do obliczeń dynamicznych, można także wykorzystać dedykowane pakiety np. MathLab
Otwarcie zasuwy nie wpływa na wartość maksymalnego prądy rozruchowego
Otwarcie zasuwy nieznacznie wydłuża rozruch agregatu pompowego (0,5s)
Otwarcie zasuwy nieznacznie zwiększa ciepło wydzielane podczas rozruchu (12,3%)
W wielu układach pompowych wzrost ciepła rozruchu o kilkanaście procent może być akceptowalny, a więc w wyjątkowych przypadkach (o ile nie ograniczają tego zjawiska dynamiczne w układzie) można pompę odśrodkową uruchamiać „na klapę” (przy otwartej zasuwie)

WARTO SPRAWDZIĆ: