Obliczenia współczynnika strat liniowych wg Colebrooka-White’a

Obliczenia współczynnika strat liniowych wg formuły Colebrooka-White’a, zgodnie z procedurą opisaną na stronie współczynnik strat liniowych, zademonstruję na przykładzie obliczeń strat pojedynczego rurociągu.

Krok 1. Dane do obliczeń

Rys. 1. Model pojedynczego rurociągu

  • Q = 60 m3/h – przepływ w rurociągu
  • d = 100 mm – średnica wewnętrzna rurociągu
  • k = 0,05 mm – chropowatość bezwzględna rurociągu, wysokość nierówności
  • ν = 1 cSt – lepkość kinematyczna (woda)
  • L = 100 m – długość rurociągu

Krok 2. Przeliczenie danych na układ SI

Namawiam, aby w obliczeniach używać wyłącznie podstawowych jednostek układu SI. Uwalnia to nas od stosowania wszelkich współczynników we wzorach obliczeniowych.

  • Q = 60 / 3600 = 0,01667 m3/s – przepływ w rurociągu
  • d = 100 / 1000 = 0,1 m – średnica wewnętrzna rurociągu
  • k = 0,05 / 1000 = 0,00005 m – chropowatość bezwzględna
  • ν = 1 / 1000000 = 0,000001  – lepkość kinematyczna

Krok 3. Obliczenia wstępne

Pole powierzchni przekroju przepływowego rurociągu

A = {\pi \cdot d^2 \over 4} = {3,14 \cdot {0,1^2} \over 4} = 0,007854

Średnia prędkość cieczy w rurociągu

v = {Q \over A} = {0,01667 \over 0,007854} = 2,12

Chropowatość względna wewnętrznej powierzchni rurociągu

e = {k \over d} = {0,00005 \over 0,1} = 0,0005

Liczba Reynoldsa

Re = {v \cdot d \over \nu} = {2,12 \cdot 0,1 \over 0,000001} = 212207

Chropowatość graniczna wg wzoru Altsula-Ljaceta

e_{gr} = {23 \over Re} = {23 \over 212207} = 0,000108

Krok 4. Sprawdzenie czy rurociąg jest hydraulicznie gładki

e=0,0005 > e_{gr} = 0,000108

Rurociąg nie jest hydraulicznie gładki. Współczynnik strat należy obliczyć z uwikłanego wzoru Colebrooka-White’a lub z przybliżonego Swamee-Jain’a.

Krok 5. Obliczenia współczynnika strat ze wzoru Colebrooka – White’a

\lambda=({-2 \cdot log( {{2,51 \over Re \cdot \sqrt \lambda} + {e \over 3,72}})})^{-2}

W programach komputerowych np. PDP (Program Doboru Pomp) do wyznaczenia wartości współczynnika wykorzystywane są metody iteracyjne. W prezentowanym przykładzie wykorzystam arkusz kalkulacyjny i bardzo prostą metodę przeszukiwania przedziału. Metoda ta daje dowolnie wysoką dokładność.

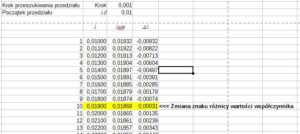
Rys. 2. Przeszukiwanie przedziału wartości współczynnika

  • Ustalam krok przeszukiwania przedziału (patrz arkusze kalkulacyjne)
  • Ustalam początek przeszukiwania przedziału
  • Przepisuję wartość początku przedziału do komórki 1
  • W kolejnych wierszach kolumny λ obliczam wartości współczynnika dodając krok do wartości w poprzednim wierszu
  • Obliczam wartość współczynnika λobl ze wzoru Colebrooka – White’a, wykorzystując wartość współczynnika z kolumny λ
  • Obliczam różnicę λ – λobl
  • Poszukiwana wartość współczynnika strat znajduje się w wierszu w którym różnica zmienia znak (żółty kolor na rys. 2)

Krok 6. Obliczenia strat rurociągu

Straty liniowe w rurociągu obliczam ze wzoru Darcy-Weisbach’a

\Delta h = {\lambda \cdot {l \over d}} \cdot {v^2 \over 2 \cdot g} = 0,019 \cdot {100 \over 0,1} \cdot {2,12^2 \over 2 \cdot 9,81} = 4,36

Arkusze kalkulacyjne:

PAMIĘTAJ

  • Chropowatość rurociągu zależy od: materiału, dokładności wykonania powierzchni wewnętrznej i czasu eksploatacji
  • Gdy zmienisz dane obliczeniowe – oblicz nowy współczynnik strat
  • Wg wzoru Colebrooka – White’a obliczamy współczynnik dla IV i V strefy

Warto sprawdzić: