WSPÓŁCZYNNIK STRAT LINIOWYCH
W okresie ubiegłych 200 lat, na podstawie wielu badań doświadczalnych, wyprowadzono dziesiątki formuł określających współczynnik oporu. R. Mizes wykazał, że wartość współczynnika oporu zależy od liczby Reynoldsa i chropowatości względnej:
\lambda=f(Re,e)
λ - współczynnik oporów liniowych, Re – liczba Reynoldsa, e - chropowatość względna wewnętrznej ściany rurociągu.
Liczba Reynoldsa określona jest wzorem:
Re={v \cdot d \over \nu}={4 \cdot Q \over \pi \cdot d \cdot \nu}
v - prędkość średnia [ m/s ] d – średnica wewnętrzna rurociągu [ m ] ν - lepkość kinematyczna płynu [ m2/s ] Q – natężenie przepływu, strumień objętości [ m3/s ]
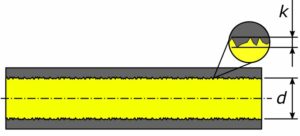
Rys. 1. Chropowatość rurociągu
Chropowatość względna określona jest wzorem:
e={k \over d}
k – chropowatość bezwzględna wewnętrznych ścian rurociągu [ m ]
Dla zobrazowania zależności, służących do obliczeń wartości współczynnika oporów, posłużymy się wykresem Moody’ego.
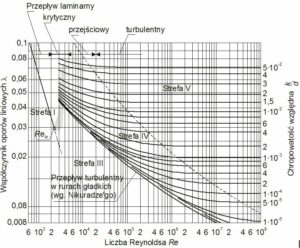
Rys. 2. Wykres Moody’ego
Przepływy przedstawione na wykresie podzielone są na 5 stref:
- I – strefa przepływów laminarnych Re <= 2320
- II – strefa przepływów niestabilnych 2320 < Re < 4000
- III – strefa przepływów turbulentnych w rurach hydraulicznie gładkich
- IV – strefa przejściowa przepływów turbulentnych w rurach chropowatych
- V – strefa przepływów turbulentnych w rurach chropowatych
W strefie I występują przepływy laminarne. Współczynnik strat jest zgodnie z prawem Hagen-Poiseulle’a i wyraża się wzorem:
\lambda={64 \over Re}
λ – współczynnik strat liniowych Re – liczba Reynoldsa
W strefie II przepływ jest nieustabilizowany. W tej strefie może występować zarówno przepływ laminarny jak i turbulentny. Nie jest zatem możliwe jednoznaczne określenie współczynnika strat liniowych.
W tej strefie, w numerycznych obliczeniach sieci, stosowana jest interpolacja Dunlopa.
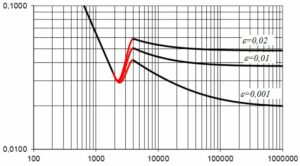
Rys. 3. Interpolacja Dunlopa
W strefie III występuje przepływ turbulentny a współczynnik strat należy obliczać ze wzoru Prandtla-Karmana:
\lambda=({2 \cdot log {\sqrt \lambda \cdot Re \over 2,51}})^{-2}
Chropowatość wewnętrznej powierzchni rury powinna być mniejsza od chropowatości granicznej:
e<e_{gr}
W strefia IV i V występuje przepływ turbulentny. Współczynnik strat należy, zgodnie z normą PN-76/M-34034, wyznaczać ze wzoru Colebrooka-White’a:
\lambda=({-2 \cdot log( {{2,51 \over Re \cdot \sqrt \lambda} + {e \over 3,72}})})^{-2}
Wzór Colebrooka-White’a ma postać uwikłaną. Wygodniej jest tu korzystać z formuł przybliżonych, np. ze wzoru Swamee i Jain:
{1 \over \sqrt \lambda}=2 \cdot log( {{5,74 \over Re^{0,9}} + {e \over 3,7}})
PAMIĘTAJ !
- W strefie I – przepływy laminarne, opory są proporcjonalne do prędkości przepływu (Q)
- W strefie V – przepływy turbulentne, opory są proporcjonalne do kwadratu prędkości przepływu (Q^2)
- W strefie IV – opory NIE są proporcjonalne do kwadratu prędkości przepływu (Q^2)
Warto sprawdzić:
- Kalkulator Oporów Przepływu 06
- Kalkulator oporów przepływu 04
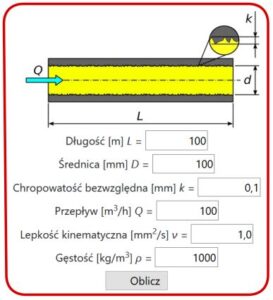
- Obliczenia – przepływ przez pojedynczy rurociąg (HydroNET)
- Obliczenia strat liniowych – wzór Darcy-Weisbacha
- Przykład obliczenia współczynnika strat liniowych wg wzoru Swamee-Jain
- Przykład obliczenia współczynnika strat liniowych wg wzoru Colebrooka-White’a
- Współczynniki strat miejscowych
- Norma PN-76/M-34034 – Zasady obliczeń strat ciśnienia
