Wybrane współczynniki strat kolan dla kątów 45°, 60°, 75°, 90°.
Kolano ostre – zmiana kierunku przepływu

Rys.1. Zmiana kierunku przepływu – kolano ostre
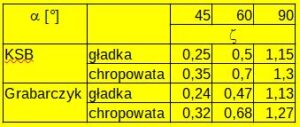
Tab.1. Wartości współczynników strat miejscowych przy zmianie kierunku wg. Grabarczyk – Przepływ cieczy w przewodach, KSB – Centrifugal Pump Lexicon
Wartości współczynników z tabeli 1 zostały aproksymowane krzywymi 2-go stopnia i pokazane na rys.2.
\zeta=C \cdot \alpha^2 (1)
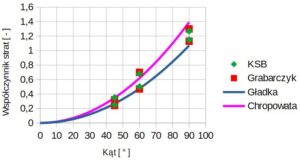
Rys.2. Aproksymacja współczynników strat miejscowych przy zmianie kierunku
Wartość współczynnika C w równaniu 1:
- dla rur gładkich – Cg = 0,0001322
- dla rur chropowatych – Cch = 0,0001719
Zakładam, że współczynnik strat zmienia się proporcjonalnie do chropowatości względnej rurociągu e = k/d.
Wartość referencyjną, opisaną w literaturze jako „ściana chropowata” przyjmuję eref = 0,01.
Ostatecznie wzór na współczynnik strat przy zmianie kierunku ma postać:
\zeta=\left[ C_g + (C_{ch} - C_g) \cdot {e \over e_{ref}} \right] \cdot \alpha^2 (2)
Kolano gięte

Rys.3. Kolana hamburskie
Promień R kolan hamburskich
R \approx 1.5 \cdot D_n (3)
R \approx 1.55 \cdot d (4)
Wartość współczynnika strat kolan giętych wg Weisbacha (za Grabarczyk – Przepływ cieczy w przewodach) określa wzór 5.
\zeta_g = \left[ 0,0131 + 0,163 \left( {R \over d} \right)^{-3,5} \right] \cdot {\alpha \over 90^\circ} (5)
Dla kolana hamburskiego 90° gładkiego, o promieniu opisanym wzorem 4, wartość współczynnika opisuje wzór 6.
\zeta_g = \left[ 0,0131 + 0,163 \cdot 1,55^{-3,5} \right] = 0,1662 (6)
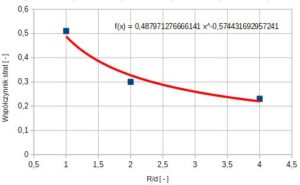
Rys.4. Aproksymacja wykładnicza współczynnika strat kolan giętych chropowatych wg Hofmana i Wasilewskiego (za Grabarczyk – Przepływ cieczy w przewodach)
Dla kolana hamburskiego chropowatego, o promieniu opisanym wzorem 4, wartość współczynnika przedstawia wzór 7.
\zeta_{ch} = 0,4879 \cdot \left( R \over d \right)^{-0,5744} = 0,4879 \cdot 1,55^{-0,5744} = 0,3793 (7)
Według Weisbach (wzór 5) współczynnik strat zmienia się liniowo z kątem wygięcia kolana. Biorąc to pod uwagę oraz wzory 6 i 7, współczynnik strat kolan giętych można opisać wzorem 8.
\zeta = \left[ \zeta_g + \left(\zeta_{ch} - \zeta_g \right) \cdot {e \over e_{ref}} \right] \cdot {\alpha \over 90^\circ} (8)
\zeta = \left[ 0,1662 + 0,2132 \cdot {e \over e_{ref}} \right] \cdot {\alpha \over 90^\circ}
Kolano segmentowe pojedyncze

Rys.5. Kolana segmentowe pojedyncze – odpowiednik kolana hamburskiego
Kąt cięcia rury φ i długość konstrukcyjną segmentu L opisują wzory 9 i 10.
\varphi = {\alpha \over 4} [9]
L = 2 \cdot R \cdot tg({\alpha \over 4}) [10]
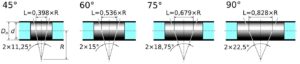
Rys.6. Wymiary kolan segmentowych pojedynczych (odpowiedniki kolan hamburskich)
Interpolację współczynnik strat na podstawie wartości z PN-76/M-34034 Tab. I-5/4 pokazano na rys. 7.
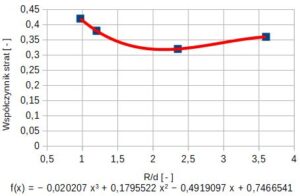
Rys.7. Współczynniki strat kolan segmentowych pojedynczych w zależności od R/d wg PN-76/M-34034
Wartość współczynnika strat dla kolana gładkiego o kącie 90° wynosi ζg = 0,3401.
Współczynnik strat dla kolan chropowatych, wg PN-76/M-34034, obliczany jest ze wzoru 11.
\zeta_{ch} = C \cdot \zeta_g (11)
Na podstawie PN-76/M-34034 Tab. I-4/2, z dokładnością wystarczającą do obliczeń inżynierskich można przyjąć Re>200000 i wartość stałej we wzorze 11 jako C ≈ 2.
Wartość współczynnika strat dla kolana chropowatego o kącie 90° wynosi: ζch = 0,6802.
Wykorzystując postulat, Weisbacha o liniowej zmianie współczynnika z katem wygięcia (wzór 5) i proporcjonalnej zmianie z chropowatoścą, współczynnik strat kolan segmentowych pojedynczych (odpowiednik kolan hamburskich) można opisać wzorem 12.
\zeta = \left[ \zeta_g + \left(\zeta_{ch} - \zeta_g \right) \cdot {e \over e_{ref}} \right] \cdot {\alpha \over 90^\circ} (12)
\zeta = \left[ 0,3401 + 0,3401 \cdot {e \over e_{ref}} \right] \cdot {\alpha \over 90^\circ}
R - promień gięcia kolana d - średnica wewnętrzna rurociągu Dn - średnica nominalna rurociągu α - kąt kolana (zmiany kierunku w stopniach °) φ - kąt cięcia rurociągu L - długość konstrukcyjna segmentu (długość w osi) C - stała k - chropowatość bezwzględna e - chropowatość względna
Wzory 2, 8 i 12 zostały wykorzystane w procedurach obliczeniowych Kalkulatora Oporów Przepływu 05.
Arkusze kalkulacyjne:
- Przykład obliczeń wybranych współczynników StratyMiejscowe.ODS
- Przykład obliczeń wybranych współczynników StratyMiejscowe.XLSX
PAMIĘTAJ
- Wykorzystane aproksymacja wartości współczynników są ważne w zakresach pokazanych na wykresach
- Długości kolan powinny być dodana do długości rurociągu
- Ograniczony wybór kształtów i przyjęte uproszczenia powodują, że uzyskane wzory końcowe nie powinny być wykorzystywane w analizach krótkich rurociągów z dużą liczbą kolan.
- Do analizy rurociągów o złożonych kształtach w węzłowych punktach układów powinno się stosować metodę analizy metodą CFD.
WARTO SPRAWDZIĆ:
- Kalkulator Oporów Przepływu v06
- Obliczenia strat miejscowych
- Obliczenia strat liniowych
- Kalkulator oporów przepływu 04
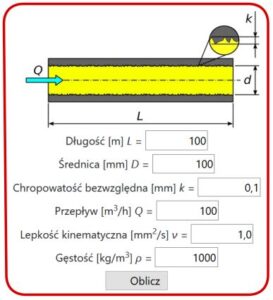
- Obliczenia – przepływ przez pojedynczy rurociąg (HydroNET)
- Obliczenia strat liniowych – wzór Darcy-Weisbacha
- Przykład obliczenia współczynnika strat liniowych wg wzoru Swamee-Jain
- Przykład obliczenia współczynnika strat liniowych wg wzoru Colebrooka-White’a
- Norma PN-76/M-34034 – Zasady obliczeń strat ciśnienia
