SUMA SZEREGOWA DWÓCH RUROCIĄGÓW
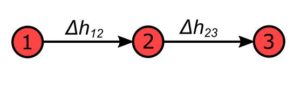
Rys. 1. Graf i połączenia szeregowego dwóch rurociągów
Załóżmy, że w węźle 2 nie ma rozbioru. Na tej podstawie możemy stwierdzić, że dla połączenia szeregowego, przepływ przez rurociąg 12 i 23 jest taki sam.
Q=Q_{12}=Q_{23}
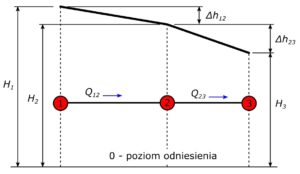
Rys. 2. Linia wysokości energii połączenia szeregowego rurociągów
Straty ciśnienia w rurociągach możemy opisać jako różnicę ciśnienia między węzłem początkowym i końcowym.
{\Delta}h_{12} = H_1 - H_2
{\Delta}h_{23} = H_2 - H_3
Calkowitą stratę połączenia szeregowego obliczamy jako sumę strat w poszczególnych elementach. Tak więc strata całkowita strata układu jest opisana wzorem.
{\Delta}h_{13} = H_1 - H_3 = {\Delta}h_{12} + {\Delta}h_{23}
W wielu przypadkach, w obliczeniach układów, możemy założyć, że charakterystyki przepływu rurociągów są funkcjami kwadratowymi o postaci:
{\Delta}h = R{\cdot} Q^2
Równanie przepływu dla sumy szeregowej rurociągów między węzłami 1 i 3 ma następującą postać:
{\Delta}h = (R_{12}+R_{23}){\cdot} Q^2
Q - przepływ Q12 - przepływ przez rurociąg między węzłami 1 i 2 Q23 - przepływ przez między węzłami 2 i 3 (suma przepływów Q23.1 i Q3.2) H1 - wysokość ciśnienia w węźle 1 H2 - wysokość ciśnienia w węźle 2 H3 - wysokość ciśnienia w węźle 3 Δh12 - strata między węzłami 1 i 2 Δh23 - strata między węzłami 2 i 3 R12 - rezystancja rurociągu między węzłami 1 i 2 R23 - rezystancja rurociągu między węzłami 2 i 3
Charakterystykę zastępczą rurociągów połączonych szeregowo możemy także wyznaczyć graficznie przez sumowanie rzędnych charakterystyk składowych dla różnych przepływów.
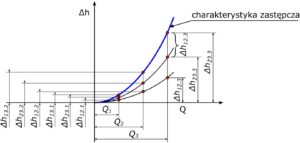
Rys.3. Suma szeregowa dwóch rurociągów
Q - przepływ Q1 - mały przepływ 1 Q2 - średni przepływ 2 Q3 - duży przepływ 3 Δh12.1, Δh12.2, Δh12.3 - strata między węzłami 1 i 2 dla różnych przepływów Δh23.1, Δh23.2, Δh23.3 - strata między węzłami 2 i 3 dla różnych przepływów
PAMIĘTAJ !
- Dla zerowego przepływu straty są zerowe, charakterystyka zawsze przechodzi przez początek układu
- Charakterystyka może być przybliżona parabolą
- Charakterystyki rurociągów i charakterystyka zastępcza, w początku układu, zawsze są styczne do osi Q (parabole)
WARTO SPRAWDZIĆ:
