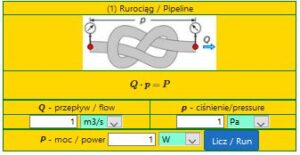
Dla sprawnego poruszania się po układach pompowych, przydatne jest zapamiętanie kilku prostych wzorów, składających się w zasadzie z trzech liter.
Używaj układu SI – wówczas we wzorach nie ma współczynników
SI - Międzynarodowy Układ Jednostek Miar (Système international d'unités) (w opisach podane są podstawowe jednostki układu)
- Energia
- Energia potencjalna
- Energia ciśnienia – praca przetłaczania
- Energia kinetyczna
- Energia cieplna
- Całkowita energia cieczy
- Moc
- Moc mechaniczna w ruchu postępowym
- Moc mechaniczna w ruchu obrotowym
- Moc hydrauliczna
- Moc cieplna
- Moc elektryczna
- Moc prądu 1-fazowego
- Moc prądu 3-fazowego
- Konwersja mocy
1. Energia
Energia jest związana z masą i określa zdolność wykonania pracy.
E = m \cdot Y (1)
E - energia (Energy) [J] m - masa [kg] Y - energia jednostkowa [J/kg]
Ze wzoru 1 wynika, że im mamy większą masę, tym więcej zakumulowanej energii.
Energia może mieć różną postać.
Energia = Praca = Energia elektryczna = Ciepło (2)
2. Energia potencjalna
Energia potencjalna to iloczyn drogi i siły.
E = F \cdot d (3)
1 J = 1N \cdot 1m (4)
E - energia (Energy) [J]
d - droga (distance) [m]
F - siła (Force) [N]
Rozpatrzmy energię, przypisaną do masy wody m, w polu grawitacyjnym Ziemi.
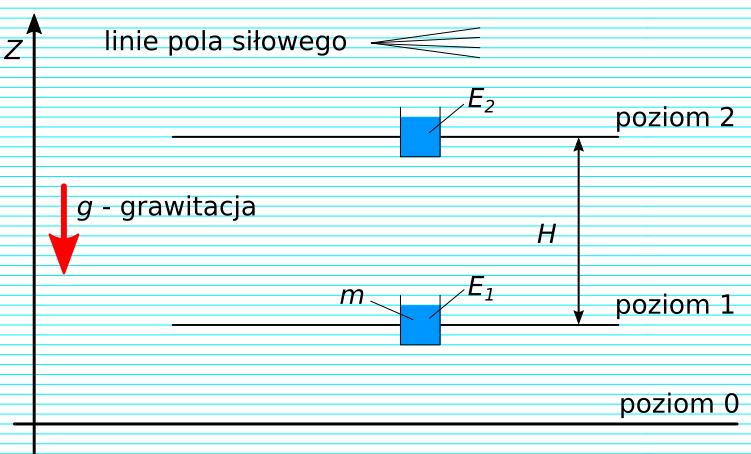
Rys. 1. Energia masy m w polu siłowym g
Dla każdej masy, znajdującej się w polu grawitacyjnym Ziemi, w odniesieniu do poziomu energetycznego ZERO, możemy napisać równanie 5.
E = F \cdot Z (5)
Siłę wywołaną grawitacją określa II zasada dynamiki Newtona, wzór 6 i 7.
F = m \cdot g (6)
F = V \cdot \rho \cdot g (7)
Z - rzędna [m] m - masa (mass) [kg] V - objętość (Volume) [m3] ρ - gęstość [kg/m3] g - przyspieszenie ziemskie (gravity) [m/s2]
Energi może być akumulowana i odzyskiwana.
Bardzo dobrym sposobem na akumulowanie energii, w skali przemysłowej, jest podnoszenie wody na wyższy poziom energetyczny.
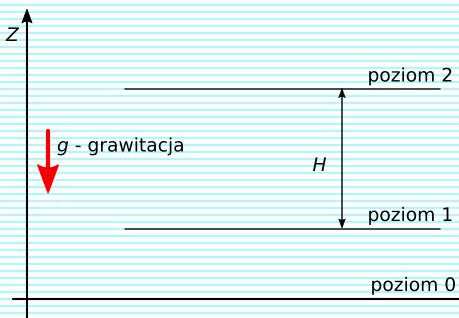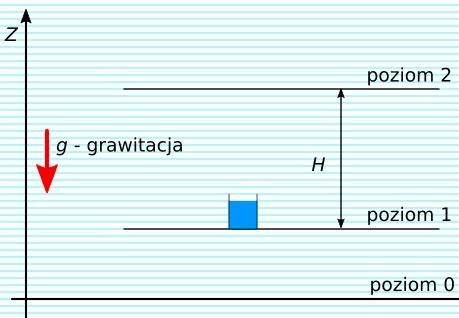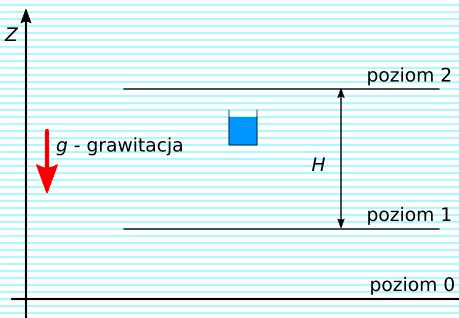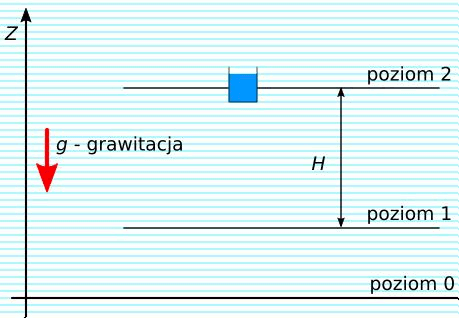
Rys. 2. Akumulacja energii w wodzie
W tym przypadku posługujemy się pojęciem wysokość podnoszenia – H, które określa różnicę poziomów w ziemskim polu grawitacyjnym.
Energa określonej objętości cieczy V o gęstości ρ, która znajduje się na wysokość H określona jest wzorem 8.
E = H \cdot V \cdot \rho \cdot g (8)
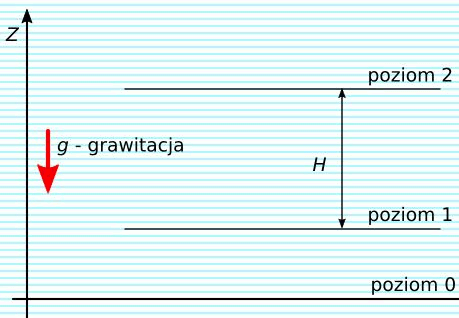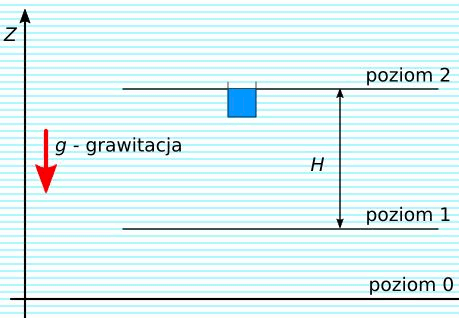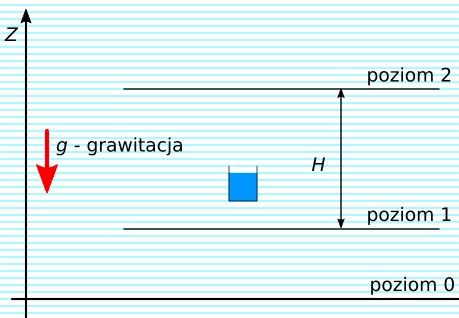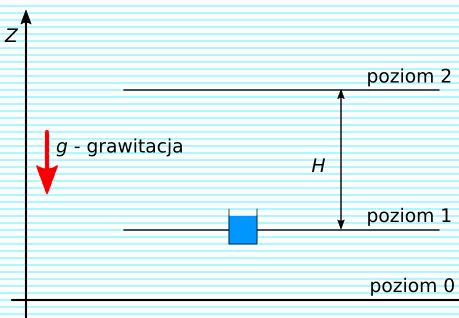
Rys. 3. Rekuperacja energii z wody
Zgromadzoną energię można odzyskać w procesie rekuperacji przez przeniesienie masy na niższy poziom energetyczny.
Na podstawie wzorów 1, 6 i 8 możemy napisać równanie definicyjne pojęcia wysokości podnoszenia H, jako odpowiednika energii jednostkowej (energii przypisanej do 1 kg masy) w ziemskim polu grawitacyjnym.
E = F \cdot d (9)
H = {Y \over g} (10)
Wysokość podnoszenia – H, ze względu na łatwość reprezentacji graficznej, jest powszechnie stosowanym pojęciem w pompach i układach pompowych.
W praktyce i literaturze można spotkać wiele odpowiedników wysokości podnoszenia:
- wysokość hydrauliczna
- spad (określenie stosowane w elektrowniach wodnych)
- wysokość energii
- wysokość prędkości
- wysokość energii kinetycznej
- wysokość energii potencjalnej
- wysokość ciśnienia
3. Energia ciśnienia
Energia ciśnienia – praca przetłaczania.
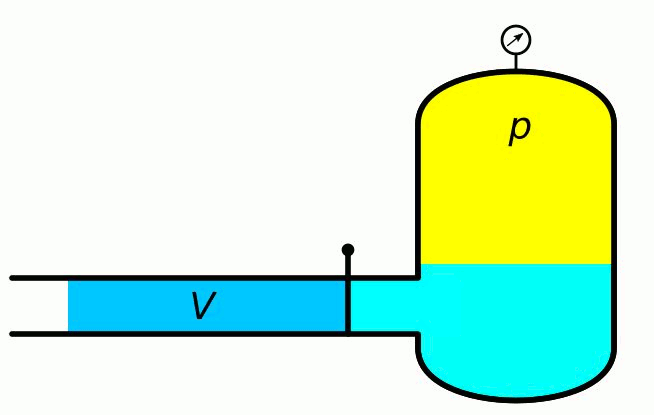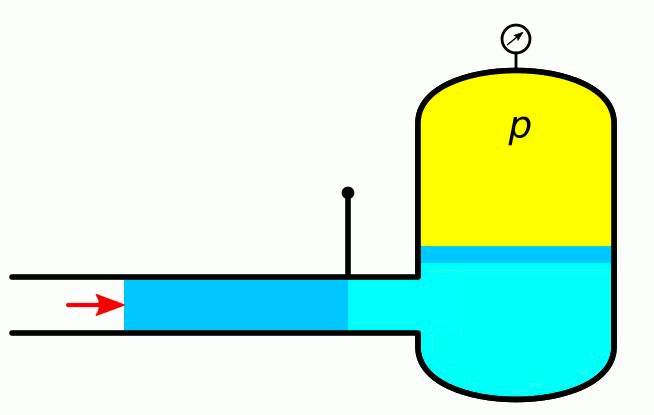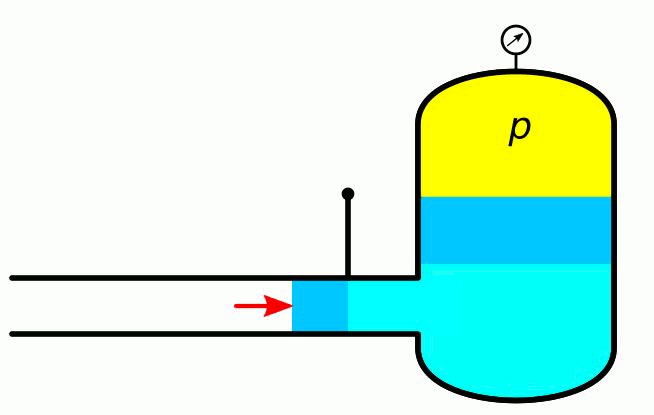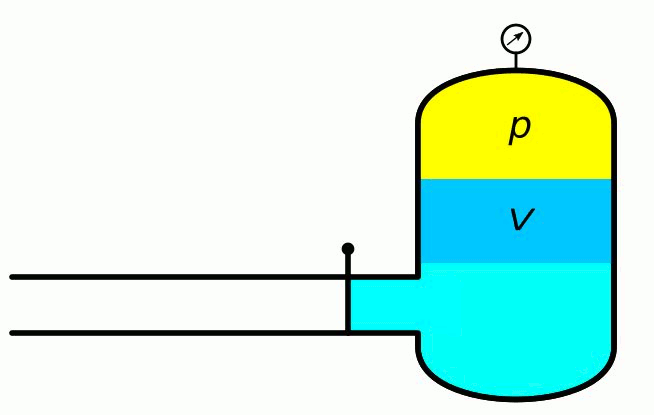
Rys. 4. Akumulator ciśnieniowy
Jeżeli w równaniu 3 siłę podzielimy a długość pomnożymy przez pole powierzchni A, to otrzymamy zależność 11, opisującą energię zgromadzoną w cieczy o objętości V, będącej pod ciśnieniem p.
E = {F \over A} \cdot ( d \cdot A) (11)
Na podstawie równania 11, po uwzględnieniu zależności na ciśnienie i objętość, otrzymamy wzór na pracę przetłaczania w postaci 12.
E = p \cdot V (12)
Energia wyrażona wzorami 8 i 12 może być zapisana wspólnie jako równanie 13.
H \cdot V \cdot \rho \cdot g = p \cdot V (13)
Po wyeliminowaniu objętości, wysokość ciśnienia określa wzór 14.
H = {p \over \rho \cdot g} (14)
E - energia (Energy) [J] V - objętość (Volume) [m3] H - wysokość (Head) [m] p - ciśnienie (pressure) [Pa] ρ - gęstość [kg/m3] g - przyspieszenie ziemskie (gravity) [m/s2]
4. Energia kinetyczna
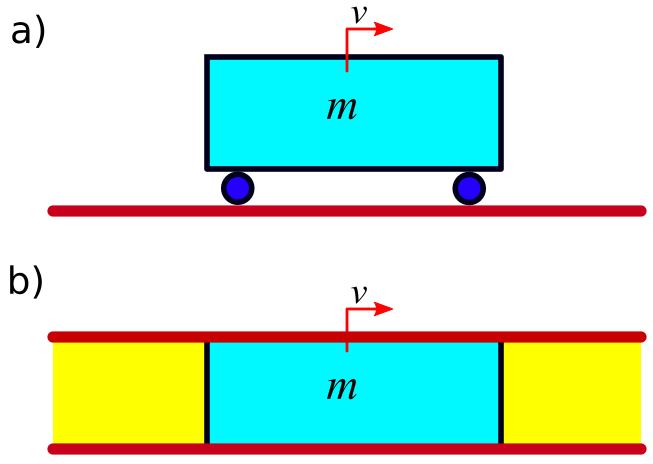
Rys. 5. Energia kinetyczna poruszającej się masy: a) ciało stałe, b) ciecz
Energia kinetyczna masy ciała opisana jest wzorem 15.
E = {m \cdot v^2 \over 2} (15)
m - masa (mass) [kg] v - prędkość (velocity) [m/s]
Na podstawie wzorów 14 i 15 możemy napisać wzór 16 na wysokość prędkości (wysokość dynamiczną, wysokość energii kinetycznej)
H = {v^2 \over 2 \cdot g} (16)
5. Energia cieplna
Energia cieplna, nazywana również energią wewnętrzną, opisana jest wzorem 17.
E = m \cdot c_p \cdot \Delta T (17)
m - masa (mass) [kg] cp - ciepło właściwe [J/deg] ΔT - różnica temperatur [°C]
6. Całkowita energia cieczy
Całkowita energia cieczy to suma: energii potencjalnej wynikającej z wysokości położenia, energii potencjalnej wynikającej z ciśnienia, energii kinetycznej i energii wewnętrznej (energii cieplnej).
E = m \cdot g \cdot Z + p \cdot V + {m \cdot v^2 \over 2} + m \cdot c_p \cdot \Delta T (18)
Po podzieleniu równania 18 przez masę cieczy, otrzymamy równanie 19 na energię jednostkową, całkowitą energię 1 kg masy.
Y = g \cdot Z + {p \over \rho} + {v^2 \over 2} + c_p \cdot \Delta T (19)
Jeżeli w obliczeniach możemy pominąć zmiany temperatury cieczy na skutek strat przepływu, to równanie na energię jednostkową zapisujemy w prostszej postaci 20.
Y = g \cdot Z + {p \over \rho} + {v^2 \over 2} (20)
Jeżeli wykorzystamy równanie definicyjne wysokości podnoszenia 10, jako substytutu energii jednostkowej, to po podzieleniu równania 20 przez przyśpieszenie ziemskie, otrzymamy równanie określające wysokość energii cieczy w postaci 21.
H = Z + {p \over \rho \cdot g} + {v^2 \over 2 \cdot g} (21)
Ostatecznie wysokość energii jest sumą: wysokości położenia, wysokości ciśnienia i wysokości prędkości.
7. Moc
Moc to zdolność wykonania pracy w określonym czasie.
P = {E \over t } (22)
Jednostką mocy jest WAT.
1 W ={1 J \over 1s} (23)
P - moc (Power) [W] E - energia, praca, ciepło (Energy) [J] t - czas (time) [s]
8. Moc mechaniczna w ruchu postępowym
Na podstawie wzorów 3 i 22 możemy napisać wzór 24 na moc w ruchu postępowym.
P = {F \cdot d \over t} (24)
Prędkość w ruchu postępowym określa wzór 25.
v = {d \over t} (25)
Na podstawie wzorów 24 i 25 możemy napisać prosty wzór 26.
P = {F \cdot v} (26)
d - droga [m] t - czas [s] v - prędkość [m/s] F - siła [N] P - moc [W]
Przykład
Jeżeli napęd na koła samochodu ma moc P=100000W, a jego prędkość wynosi v=40m/s to opory ruchu wynoszą:
F = P/v = 100000/40 = 2500N
9. Moc mechaniczna w ruchu obrotowym
Prędkość w ruchu obrotowym i moment siły określone są wzorami 27 i 28.
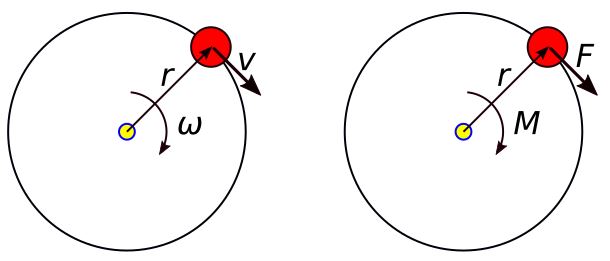
Rys. 6. Prędkość obwodowa i moment siły
v = \omega \cdot r (27)
M = F \cdot r (28)
W równaniu 26 siłę F mnożymy, a prędkość v dzielimy przez promień r.
P = F \cdot r \cdot {v \over r} (29)
Ostatecznie równanie 29, po uwzględnieniu zależności 27 i 28, możemy zapisać w postaci 30.
P = {M \cdot \omega} (30)
v - prędkość [m/s] ω - prędkość kątowa [1/s] F - siła [N] r - promień (radius) [m] M - moment [Nm] P - moc [W]
Przykład
Jeżeli silnik elektryczny ma moc P=3000W, a prędkość kątowa jego wału jest ω=300 1/s to moment skręcający wału wynosi:
M = P/ω = 3000/300 = 10 N
10. Moc hydrauliczna
W równaniu 26 siłę F dzielimy, a prędkość v mnożymy przez pole powierzchni przekroju A.
P = {F \over A} \cdot v \cdot A (31)
Składniki po prawej stronie równania 31 możemy zapisać jako ciśnienie 32 i przepływ 33.
p = {F \over A} (32)
Q = v \cdot A (33)
Ostatecznie proste równanie, określające moc hydrauliczną ma postać 34.
P = p \cdot Q (34)
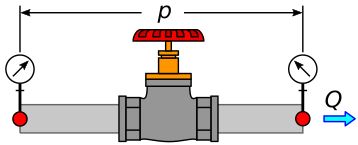
Rys. 7. Moc strat hydraulicznych
v - prędkość [m/s] F - siła [N] A - pole powierzchni (Area) [m2] p - ciśnienie (pressure) [Pa] Q - przepływ [m3/s] P - moc [W]
Przykład
Jeżeli strata ciśnienia na zaworze wynosi p=10000000 Pa, a przepływ przez zawór wynosi Q=0,01 m3/s, to moc strat na zaworze wynosi:
P = 10000000 * 0,01 = 100000 W = 100 kW
Moc hydrauliczną cieczy przemieszczanej w ziemskim polu grawitacyjnym, z wykorzystaniem pojęcia wysokości podnoszenia, pokazuje równanie 35.
P = H \cdot \rho \cdot g \cdot Q (35)
H - wysokość podnoszenia lub spad [m] ρ - gęstość [kg/m3] g - przyspieszenie ziemskie [m/s2] Q - przepływ [m3/s] P - moc [W]
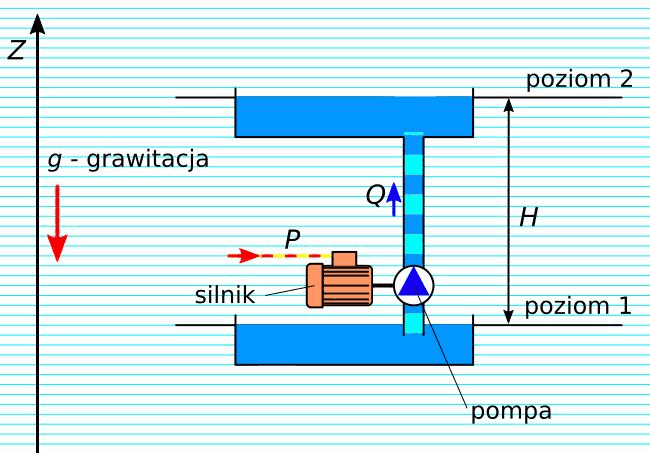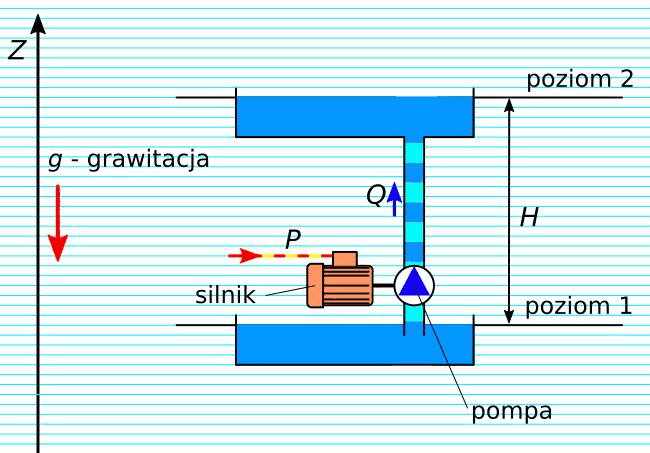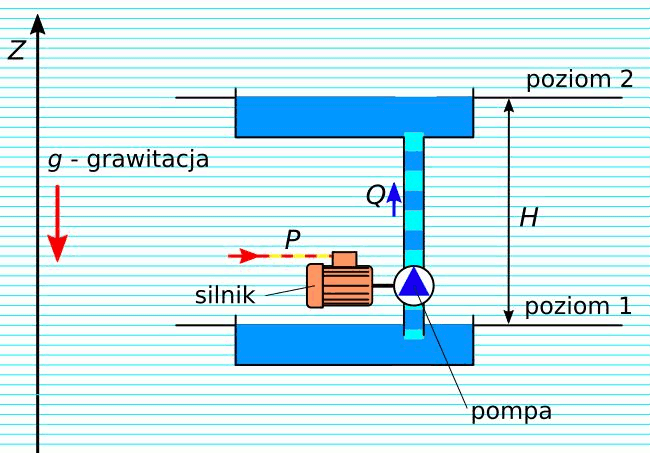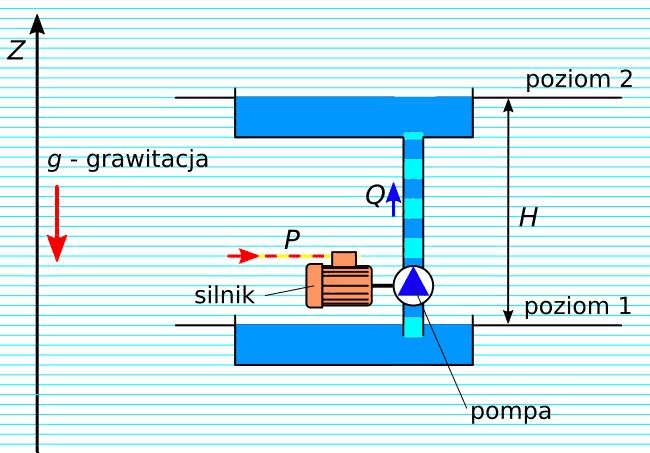
Rys. 7. Zamiana mocy elektrycznej na hydrauliczną – układ pompowy
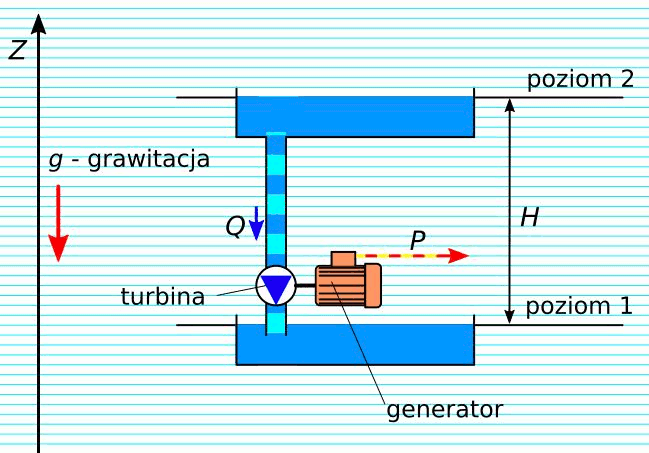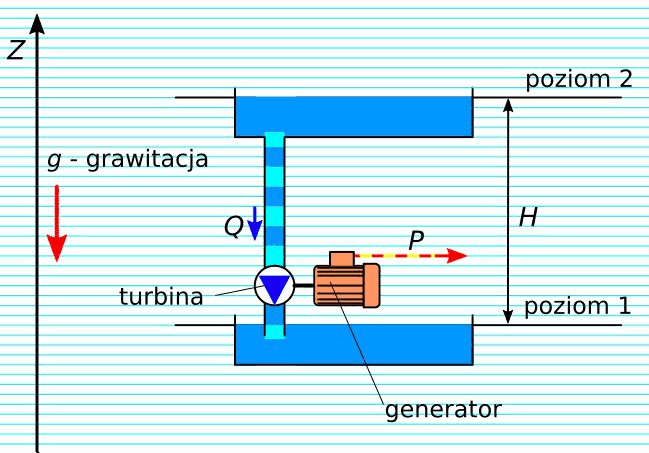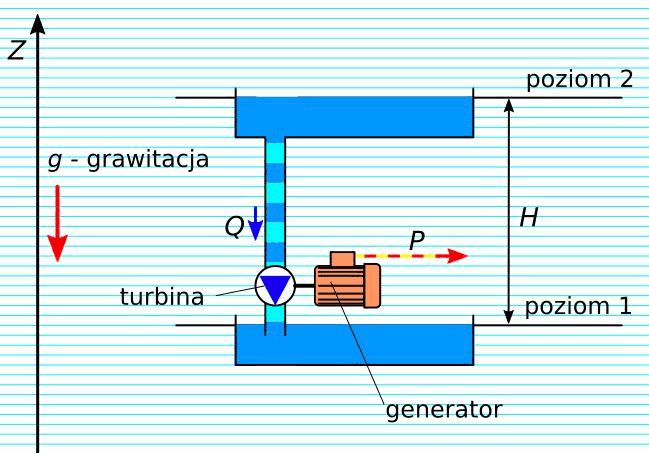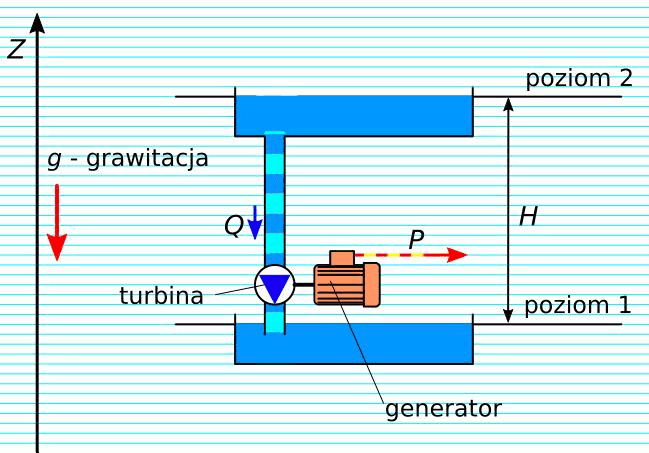
Rys. 8. Zamiana mocy hydraulicznej na elektryczną – elektrownia wodna
Przykład
Jeżeli różnica poziomów między zbiornikami - spad wynosi H=100 m, a przepływ wody między nimi Q=1 m3/s, to moc hydrauliczna (moc surowa) wynosi:
P = 100 * 1000 * 9,81 * 1 = 981000 W = 981 kW
11. Moc cieplna
Na podstawie wzorów 17 i 22 możemy napisać równanie na moc cieplną 36.
P = {E \over t} ={m \over t} \cdot c_p \cdot \Delta T = {V \cdot \rho \over t} \cdot c_p \cdot \Delta T (36)
Ostatecznie, po uwzględnieniu wzoru na przepływ, moc cieplna opisana jest zależnością 37.
P = Q \cdot \rho \cdot c_p \cdot \Delta T (37)
P - moc [W] m - masa (mass) [kg] V - objętość [m3] ρ - gęstość [kg/m3] cp - ciepło właściwe [J/°C] ΔT - różnica temperatur [°C]
Przykład
Jeżeli przez zawór płynie woda o gęstości ρ=1000 kg/m3 i cp=4189,9 J/kg/°C oraz natężeniu Q=0,01 m3/s, a moc strat na zaworze ma wartość P=100000 W to temperatura za zaworem wzrośnie o:
ΔT = 100000/(0,01 * 1000 * 4189,9) = 2,39 °C
12. Moc elektryczna
P = U \cdot I (38)
P - moc [W] U - napięcie [V] I - prąd [A]
Przykład
Jeżeli napięcie źródła (akumulatora) wynosi U=12 V, a pobierany prąd przez rozrusznik ma wartość I=50 A, to moc wynosi:
P = 12 * 50 = 600 W
13. Moc prądu 1-fazowego
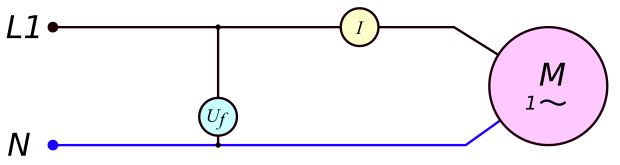
Rys. 9. Moc elektryczna pobierana przez silnik 1-fazowy
P = U_f \cdot I \cdot cos(\varphi) (39)
P - moc [W] Uf - napięcie [V] I - prąd [A] cos(φ) - współczynnik mocy [-]
Przykład
Jeżeli przez przewód zasilający płynie prąd o natężeniu I=10 A, a napięcie fazowe sieci wynosi Uf=230 V to dla silnika o współczynniku mocy cos(φ) = 0,95 moc pobierana przez silnik 1-fazowy ma wartość:
P = 230 * 10 * 0,95 = 2185 W
14. Moc prądu 3-fazowego
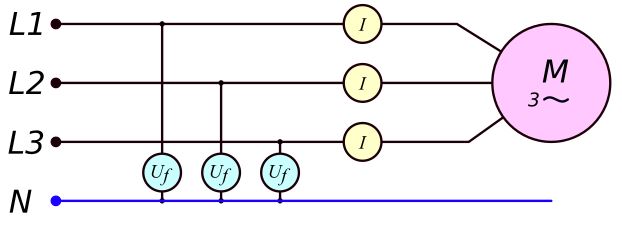
Rys. 10. Moc elektryczna pobierana przez silnik 3-fazowy
P = U_f \cdot i \cdot cos(\varphi) \cdot 3 (40)
P - moc [W] Uf - napięcie [V] I - prąd [A] cos(φ) - współczynnik mocy [-]
Przykład
Jeżeli przez przewody zasilające płynie prąd o natężeniu I=10 A, a napięcie fazowe sieci wynosi Uf=230 V, to dla silnika o współczynniku mocy cos(φ) = 0,95 moc pobierana przez silnik 3-fazowy ma wartość:
P = 230 * 10 * 3 * 0,95 = 6555 W
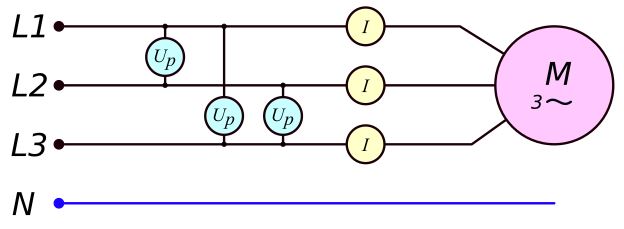
Rys. 11. Moc elektryczna pobierana przez silnik 3-fazowy
P = U_p \cdot i \cdot cos(\varphi) \cdot \sqrt{3} (41)
Przykład
Jeżeli przez przewody zasilające płynie prąd o natężeniu I=10 A, a napięcie międzyprzewodowe sieci wynosi Up=400 V, to dla silnika o współczynniku mocy cos(φ) = 0,95 moc pobierana ma wartość:
P = 400 * 10 * 3^0,5 * 0,95 = 6582 W
15. Konwersja mocy
Energia i moc nie może zniknąć, może jedynie zamienić się w inną formę.

Rys. 12. Zamiana moc elektrycznej na hydrauliczną
U_p \cdot I \cdot cos(\varphi) \cdot \sqrt{3} = P = M \cdot \omega = P = Q \cdot H \cdot \rho \cdot g (42)
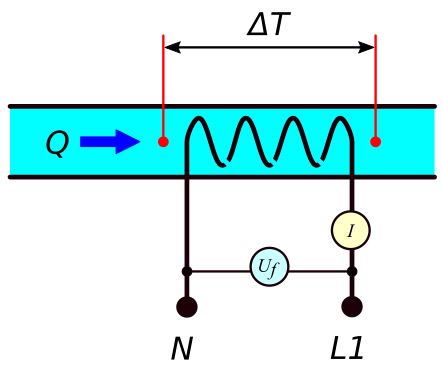
Rys. 13. Zamiana moc elektrycznej na cieplną
U_f \cdot I = P = Q \cdot \rho \cdot c_p \cdot \Delta T (43)
PAMIĘTAJ
- Chcesz unikać pomyłek – używaj w obliczeniach jedynie podstawowych jednostek układu SI: m-metr, s-sekunda, kg-kilogram, A-amper, V-volt, J-dżul, N-newton, Pa – paskal, wówczas we wzorach nie ma żadnych współczynników
- W równaniach pominięto sprawności przemian energii i mocy
- Na podstawie dobrej praktyki inżynierskiej, w wielu przypadkach można pominąć lub oszacować sprawności przemian energetycznych. Trzeba tylko wiedzieć kiedy „można”
- Dla nauczyciela fizyki wyrażenie energii w metrach jest niedopuszczalne, jednak dla świadomego inżyniera, który zna definicję wysokości podnoszenia (wzór 10) jako odpowiednika energii jednostkowej, wyrażenie energii 1 kg masy w polu grawitacyjnym Ziemi w metrach jest oczywiste
- Określenie „przekazywanie mocy” nie jest poprawne, ale dobrze opisuje przekazywanie energii
- Moc silnika elektrycznego to moc mechaniczna na wale. Moc ta zależy od obciążenia, a nie od tego, co przeczytamy na tabliczce znamionowej
WARTO SPRAWDZIĆ: