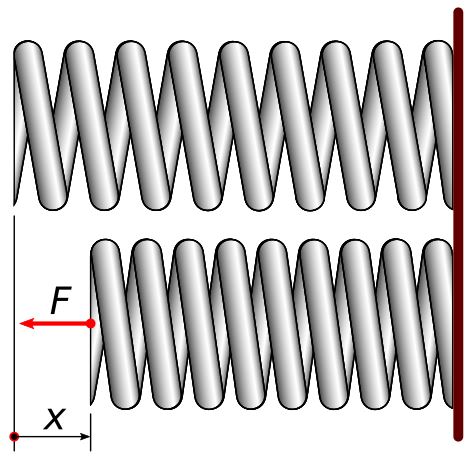
Rys.1. Sztywność sprężyny
Do przemieszczenie swobodnego końca sprężyny o wartość x potrzebna jest siła F. Stosunek tej siły F do przemieszczenia x opisuje współczynnik sztywności (sprężystości) k. Wartość tego współczynnika można wyliczyć ze wzoru 1.
k={- F \over x} (1)
k - współczynnik sztywności F - siła x - przemieszczenie
Uwaga: Zwrot siły jest odwrotny do przemieszczenia
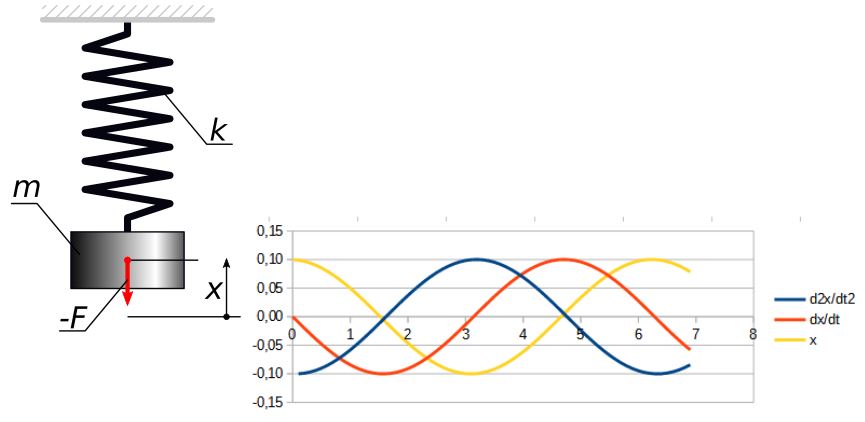
Rys.2. Przyśpieszenie, prędkość i droga masy na sprężynie
Przyśpieszenie masy m swobodnie zawieszonej na sprężynie o sztywności k (bez uwzględnienia tarcia) opisuje proste równanie różniczkowe 2.
{d2x \over {dt2}} = - {1 \over m} \cdot k \cdot x (2)
d2x/dt2 - przyśpieszenie, druga pochodna przemieszczenia po czasie dx/dt - prędkość x - przemieszczenie
Zmiany: przemieszczenia x, prędkości dx/dt i przyśpieszenia d2x/dt2 masy m można wyznaczyć przez całowanie równania 2 jak to pokazano na przykładzie, rys 3.
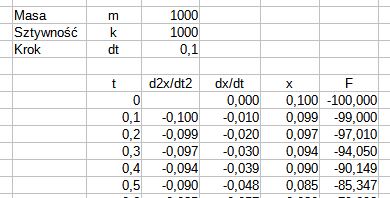 Rys.3. Symulacja drgań masy na sprężynie (kliknij aby pobrać plik)
Rys.3. Symulacja drgań masy na sprężynie (kliknij aby pobrać plik)
Przykład obliczeniowy w arkuszu kalkulacyjnym – Masa_na_sprezynie.ods.
Częstotliwość drgań harmonicznych układu pokazanego na rys. 2 można wyznaczyć ze wzoru 3.
f={n \over t} (3)
f - częstotliwość n - liczba cykli w czasie obserwacji t - czas obserwacji
Częstotliwość własną (rezonansową) układu masa-sprężyna można także wyznaczyć analitycznie ze wzoru 4.
f={1 \over 2 \cdot \pi} \cdot \sqrt{k \over m} (4)
k - współczynnik sprężystości sprężyny m - masa π - liczba pi
PAMIĘTAJ !
- Częstotliwość drgań własnych f jest równa częstotliwości rezonansowej fr tylko wtedy gdy w układzie nie ma tarcia.
Warto sprawdzić:
