Regulacja pompy przez zmianę prędkości obrotowej

Najpowszechniejszym sposobem regulacji pomp jest regulacja przez zmianę prędkości obrotowej wirnika. Popularność tej metody wynika z tego, że oprócz tradycyjnie stosowanych silników zmienno-obrotowych oraz sprzęgieł o regulowanym poślizgu i przekładni, w ostatnich latach znacząco wzrosła liczba napędów z regulacją elektroniczną. Stało się to możliwe na skutek znacznego postępu w konstrukcjach przemienników częstotliwości i obniżce cen.

Podstawy regulacji pompy, przez zmianę prędkości obrotowej, wynikają z teorii podobieństwa maszyn wirowych.

Zasady teorii podobieństwa zastosujemy dla tej samej pompy, pracującej przy różnych prędkościach obrotowych. Oznacza to, że we wszystkich rozpatrywanych przypadkach, pompa jest geometrycznie podobna i ma jednakowy wymiar charakterystyczny – średnicę wirnika d. Na tej podstawie możemy przyjąć, że prawa podobieństwa hydrodynamicznego redukują się do następującej postaci:

Q \sim n \cdot d^3 \to Q \sim n (1)

H \sim n^2 \cdot d^2 \to H \sim n^2 (2)

P \sim \rho \cdot n^3 \cdot d^5 \to P \sim \rho \cdot n^3 (3)

Wyrażenia (1) do (3) określają zmiany parametrów pracy, w zależności od prędkości obrotowej, przy założeniu, że w odpowiadających sobie punktach (punktach homologicznych) sprawność pompy się nie zmienia.

Na podstawie wzorów (1) i (2), po wyeliminowaniu prędkości obrotowej, możemy napisać wzór na krzywą, łączącą punkty homologiczne charakterystyk przepływu, w postaci:

H = C \cdot Q^2 (4)

Ze wzoru (4) wynika, że teoretyczne krzywe stałej sprawności są parabolami 2-go stopnia z minimum w początku układu współrzędnych.

Na podstawie wzorów (1) i (3) możemy napisać wzór na krzywą, łączącą punkty homologiczne charakterystyk mocy:

P = C \cdot Q^3 (5)

Q - wydajność H - wysokość podnoszenia
P - moc
d - średnica zewnętrzna wirnika
n - prędkości obrotowaC - stała

Ze wzoru (5) wynika, że teoretyczne krzywe stałej sprawności, we współrzędnych P-Q, są parabolami 3-go stopnia.

Teoretyczny przebieg charakterystyk przepływu, mocy i sprawności pokazano na rys. 6.20

Rys. 1. Powinowactwo charakterystyk przy zmianie prędkości obrotowej

a) charakterystyka przepływu, b) charakterystyka mocy, c) charakterystyka sprawności

W rzeczywistości, przy zmianie prędkości obrotowej, zmienia się także sprawność pompy. Powszechnie uznaje się, że przy niewielkich zmianach prędkości obrotowej, rzędu 10 do 20%, zmiany sprawności są pomijalne. Dla większych zmian prędkości błędy przeliczeń są istotne. W takich przypadkach należy w obliczeniach uwzględnić zmiany sprawności pompy.

Poniżej zestawiono wzory i zakresy ich stosowalności, pozwalające na przeliczenie pierwotnych parametrów pompy Q1, H1 i P1 na Q2, H2 i P2, przy zmianie prędkości obrotowej z n1 na n2.

Wydajność zmienia się według wzoru (6).

0,5 < {n_2 \over n_1} < 1,5 \ \ \ \ \ {Q_2 \over Q_1} = {n_2 \over n_1} (6)

Dla większych zmian prędkości obrotowej, zmiany sprawności objętościowej ηV istotnie wpływają na wynik przeliczeń. Konieczne jest tu skorygowanie wyników o stosunek tych sprawności według wzoru (7).

{Q_2 \over Q_1} = {n_2 \over n_1} {\eta_{V2} \over \eta_{V1}} (7)

Wysokość podnoszenia zmienia się według wzoru (8).

0,65 < {n_2 \over n_1} < 1,35 \ \ \ \ \ {H_2 \over H_1} = \left(n_2 \over n_1 \right)^2 (8)

Przedział dopuszczalnego zakresu przeliczeń wysokości podnoszenia, bez korekty (8) jest mniejszy niż dla wydajności (6), ze względu na większą zmienność sprawności hydraulicznej ηh. Dla zmian spoza tego przedziału skorygowanie wysokości podnoszenia oblicza się ze wzoru (9).

{H_2 \over H_1} = \left(n_2 \over n_1 \right)^2 {\eta_{h2} \over \eta_{h1}} (9)

Moc zmienia się według wzoru (10).

0,85 < {n_2 \over n_1} < 1,15 \ \ \ \ \ {P_2 \over P_1} = \left(n_2 \over n_1 \right)^3 (10)

Jak pokazano, najmniejszy zakres stosowalności ma wzór (10), na przeliczenie mocy pobieranej przez pompę, w porównaniu do wzoru (6) i (8). Poza tym zakresem, konieczna jest korekta wyników zgodnie ze wzorem (11).

{P_2 \over P_1} = \left(n_2 \over n_1 \right)^3 {\eta_1 \over \eta_2} (11)

W.Jędral proponuje wzory empiryczne (12) i (13), na obliczenie stosunku sprawności pomp, przy zmianie prędkości obrotowej.

{n_2 \over n_1} \ge 0,5 \ \ \ \ \ {\eta_2 \over \eta_1} = \left(n_2 \over n_1 \right)^{0,09} (12)

{n_2 \over n_1} < 0,5 \ \ \ \ \ {\eta_2 \over \eta_1} = 1,11 \cdot \left(n_2 \over n_1 \right)^{0,24} (13)

Złożony postulat W.Jędrala, zmiany sprawności ze zmianą prędkości obrotowej, wzory (12) i (13), może być z wystarczającą dokładnością zastąpiony ciągłą funkcją (14).

dla 0,2 < {n_2 \over n_1} < 1,3

{\eta_2 \over \eta_1} = 0,321124 \cdot \left(n_2 \over n_1 \right)^3 - 1,0264 \cdot \left( n_2 \over n_1 \right)^2 + 1,131 \cdot \left(n_2 \over n_1 \right) + 0,576 (14)

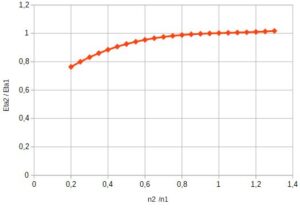
Rys. 2. Względna sprawność w zależności od względnej zmiany prędkości obrotowej wg wzoru (14)

Funkcja (14) jest wygodniejsza np. przy tworzeniu arkuszy kalkulacyjnych do przeliczania charakterystyk.

Rzeczywiste zmiany parametrów pomp są zapisywane w postaci pęków charakterystyk przepływu i mocy, dla różnych prędkości obrotowych. Na ich podstawie budowane są trójwymiarowe powierzchnie charakterystyk.

Wartości pośrednie między zmierzonymi charakterystykami są wyznaczane w sposób pokazany na rys.3.

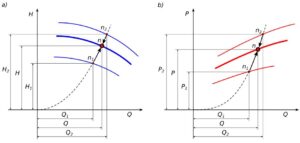
Rys. 3. Interpolacja charakterystyk pompy

Dowolne parametry pompy, między sąsiednimi charakterystykami, są interpolowane jako średnie ważone przeliczeń punktów homologicznych z obu krzywych, według następujących zależności.

Dla przeliczania wydajności:

Q_1^* = Q_1 {n \over n_1} (15)

Q_2^* = Q_2 {n \over n_2} (16)

Q = {Q_1^* \cdot (n_2 - n) + Q_2^* \cdot (n - n_1) \over n_2 - n_1} (17)

Q1, Q2 - wydajności z pomiaru
Q1*, Q2* - wydajności przeliczone
n1, n2 - prędkości obrotowe z pomiaru
n - przeliczeniowa prędkość obrotowa
Q - wydajność uśredniona

Dla przeliczania wysokości podnoszenia:

H_1^* = H_1 \left( n \over n_1 \right)^2 (18)

H_2^* = H_2 \left( n \over n_2 \right)^2 (19)

H = {H_1^* \cdot (n_2 - n) + H_2^* \cdot (n - n_1) \over n_2 - n_1} (20)

H1, H2 - wysokości podnoszenia z pomiaru
H1*, H2* - wysokości przeliczone
n1, n2 - prędkości obrotowe z pomiaru
n - przeliczeniowa prędkość obrotowa
H - uśredniona wysokość podnoszenia

Dla przeliczania mocy:

P_1^* = P_1 \left( n \over n_1 \right)^3 (21)

P_2^* = P_2 \left( n \over n_2 \right)^3 (22)

P = {P_1^* \cdot (n_2 - n) + P_2^* \cdot (n - n_1) \over n_2 - n_1} (23)

P1, P2 - moc z pomiaru
P1*, P2* - moce przeliczone
n1, n2 - prędkości obrotowe z pomiaru
n - przeliczeniowa prędkość obrotowa
P - moc uśredniona

Przedstawiona metoda przeliczania pozwala na określanie parametrów pompy, z uwzględnieniem zmian sprawności. Na tej podstawie możliwe jest także automatyczne budowanie charakterystyk muszlowych pomp, patrz rys. 4.

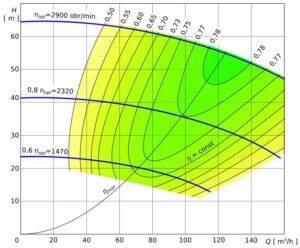
Rys. 4. Charakterystyka muszlowa pompy odśrodkowej

PAMIĘTAJ !

  • Zmiana prędkości obrotowej zmienia charakterystyki pompy
  • Zmiana prędkości obrotowej nie zmienia charakterystyki układu
  • Jeżeli masz charakterystyki dla jednej prędkości obrotowej – użyj do przeliczeń wzory 6, 8, 10
  • Sprawność pompy zmienia się z prędkością obrotową, wzory (12) i (13)
  • Nie przekraczaj zakresu stosowalności wzoru (14) (wielomiany „zaginają” się na końcach i generują duże błędy)
  • Sprawność pompy zmienia się z prędkością obrotową
  • Jeżeli masz charakterystyki dla dwóch prędkości obrotowych – użyj do przeliczeń wzory 15 – 23

Warto sprawdzić: