Najczęściej stosowanym sposobem dopasowania parametrów pomp do wymagań układu jest obtaczanie średnicy zewnętrznej wirnika. Metoda ta jest stosowana do wirników pomp odśrodkowych, helikoidalnych i diagonalnych. Ze względu na jej prostotę, zabieg zmiany średnicy wirnika pompy jest często wykonywany przez użytkownika pomp.
Przy wyznaczaniu podstawowych zależności, opisujących zmiany parametrów pomp przy obtaczaniu wirnika, możemy się posiłkować teorią podobieństwa maszyn wirowych. Wymiary i trójkąty prędkości na wylocie wirnika odśrodkowego pokazano na rys. 1.
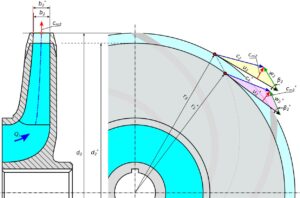
Rys.1. Obtaczanie wirnika pompy odśrodkowej
Jak wynika z rysunku, przy zmianie średnicy wirnika z d2 na d2*, szerokość wirnika b2 praktycznie pozostaje stała. Ponadto kąty łopatek β u wylotu wirnika zmieniają się w bardzo niewielkim stopniu. Na tej podstawie można sformułować następujące zależności:
b_2^* \approx b_2 (1)
\beta_2^* \approx \beta_2 (2)
b2 – szerokość wirnika na wylocie
b*2 - szerokość wirnika na wylocie po obtoczeniu
β2 – kąt łopatki na wylocie
β*2 – kąt łopatki na wylocie po obtoczeniu
u = r \cdot \omega (3)
Przy równych kątach łopatek wirnika zachodzi podobieństwo trójkątów prędkości na wylocie, jak to pokazano na rys. 2.
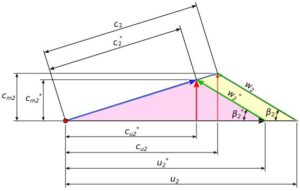
Rys.2. Trójkąty prędkości na wylocie
Jeśli przyjmiemy, że prędkość kątowa nie ulega zmianie, to prędkość unoszenia, wzór 3, i prędkość merydionalna będzie proporcjonalna do średnicy wirnika.
{d_2^* \over d_2} = {u_2^* \over u_2} = {c_{m2}^* \over c_{m2}} (4)
Dla stałej szerokości wirnika przekrój przepływowy na wylocie będzie także proporcjonalny do średnicy wirnika.
{\pi \cdot d_2^* \cdot b_2 \over \pi \cdot d_2 \cdot b_2} = {d_2^* \over d_2} = {A_2^* \over A_2} (5)
A2 – pole powierzchni wirnika na wylocie A2* – pole powierzchni wirnika na wylocie po obtoczeniu b2 – szerokość wirnika na wylocie b2* - szerokość wirnika na wylocie po obtoczeniu d2 – średnica wirnika na wylocie d2* - średnica wirnika na wylocie po obtoczeniu
Z przeprowadzonego rozumowania wynika, że przy stoczeniu wirnika, wydajność pompy zmienia się z kwadratem średnicy wirnika.
Q = A \cdot c_m \approx d \cdot d (6)
Po uwzględnieniu zależności 6 w równaniach podobieństwa oraz przy założeniu stałej prędkości kątowej, otrzymamy następujące zależności na zmianę parametrów przy zmianie średnicy wirnika:
Q \approx d^2 (7)
H \approx d^2 (8)
P \approx \rho \cdot d^4 (9)
M \approx \rho \cdot d^4 (10)
Na podstawie wzorów 7 i 8, po wyeliminowaniu średnicy, możemy napisać wzór na linię łączącą punkty homologiczne charakterystyk przepływu, o tej samej sprawności, w postaci:
H = C \cdot Q (11)
Ze wzoru 11 wynika, że linie te są prostymi, przechodzącymi przez początek układu współrzędnych, patrz rys. 2.
Na podobnej zasadzie, na podstawie wzorów 7 i 9 możemy napisać wzór na linię łączącą punkty homologiczne charakterystyk mocy:
P = C \cdot Q^2 (12)
C - stała
Jak widzimy, krzywe stałej sprawności we współrzędnych P-Q są parabolami 2-go stopnia.
Teoretyczny przebieg charakterystyk przepływu, mocy i sprawności, przy zmianie średnicy pokazano na rys. 2.

Rys.3. Zmiany charakterystyk przy obtaczaniu wirnika pompy odśrodkowej
a) charakterystyka przepływu, b) charakterystyka mocy, c) charakterystyka sprawności
Poniżej zestawiono wzory, pozwalający na przeliczenie pierwotnych parametrów pompy Q1, H1 i P1 na Q2, H2 i P2 przy obtoczeniu średnicy wirnika z d2 na d2*.
{Q_2 \over Q_1} = {H_2 \over H_1} = \left( d_2^* \over d_2 \right)^2 (13)
{P_2 \over P_1} = \left( d_2^* \over d_2 \right)^4 (14)
Z założeń teorii podobieństwa maszyn wirowych wynika, że sprawność pompy się nie zmienia, patrz rys. 2.c, jednak w rzeczywistości, przy obtaczaniu wirnika zmienia się także sprawność pompy. Dla pomp wirowych odśrodkowych (nq < 30), przy zmniejszaniu średnicy do 15(20)% zmiany są niewielkie i mogą być pominięte.
Aby uniknąć sytuacji, w której dokonano stoczenia wirnika, a po uruchomieniu pompy parametry układu są za niskie, W.Jędral Pompy wirowe zaproponował współczynnik korekcyjny we wzorze na różnicę średnic:
\Delta d_2 = k \cdot ( d_2 - d_2^*) (15)
k=0,80 \div 0,85 \ \ dla \ \ n_q \le 20
k=0,75 \div 0,80 \ \ dla \ \ n_q > 20
Δd2 - zmniejszenie średnicy zewnętrznej k - współczynnik korekcyjny
Rzeczywiste zmiany parametrów pompy przy obtaczaniu – zmianie średnicy, zwykle są przedstawiane w postaci charakterystyki muszlowej, której przykład przedstawiono na rys.4.
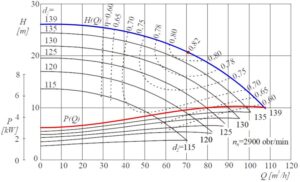
Rys.4. Wykres muszlowy pompy o wyróżniku szybkobieżności nq = 41.3
PAMIĘTAJ !
- Aby nie popełnić błędów przy obtaczaniu wirnika, należy każdorazowo, na podstawie rzeczywistych charakterystyk pompy i charakterystyki układu, przeprowadzić analizę położenia optymalnego punktu pracy układu.
Warto sprawdzić:
- Podstawowe wzory podobieństwa maszyn przepływowych
- Dopasowanie pompy przez obtaczanie wirnika
- Analiza pracy układu przy obtaczaniu wirnika pompy
