Obliczenie uderzenia hydraulicznego w pochyłym rurociągu, po awaryjnym wyłączeniu pompy, omówię na podstawie prostego przykładu. Pokażę także, jak prostymi metodami można określić zmiany przepływu i ciśnienia w czasie.
1. Dane wejściowe
Analizowany rurociąg ma długość 5000m, średnicę DN400 i jest wykonany z PE100.
Rurociąg składa się z 5-ciu odcinków o długości L= 1000m każdy. Rurociąg wznosi się równomiernie o 50m na każde 1000m. Długości odcinków i rzędne w węzłach pokazane są na rys.1.

Rys.1. Długości odcinków L [m] i rzędne węzłów Rz [m] rurociągu
Ciśnienie pracy rurociągu maleje wraz z odległością od pompy, co pozwala na zastosowanie rur o różnych ciśnieniach nominalnych, od PN32 do PN12.5.
Średnice wewnętrzne odcinków i ciśnienia w węzłach, przy przepływie Q=500 m3/h, pokazano na rys.2. Obliczenia przeprowadzono w programie HydroSKO.

Rys.2. Średnice wewnętrzne odcinków d [mm] i ciśnienia w węzłach p [bar]
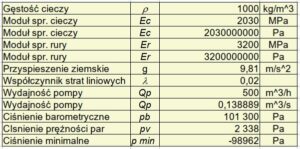
Parametry cieczy i materiału rurociągu zestawiono w tab.1. Dla ułatwienia, w obliczeniach posługuję się wyłącznie jednostkami z jednolitego systemu miar SI.
Tab.1. Parametry cieczy i rurociągu
2. Obliczenia stałych i warunków początkowych w równaniach ruchu
Zakładam, że model obliczeniowy będzie się składał z 5 elementów o długości L=1000m każdy. Elementy odpowiadają odcinkom rurociągu o jednakowym ciśnieniu nominalnym.
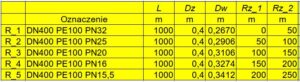
Parametry odcinków rurociągu zestawiono w tab.2.
Tab.2. Parametry elementów rurociągu
Obliczamy kolejno wartości stałe dla każdego elementu:
- grubość ścianki
e_1 = {D_z - D_w \over 2} = {0,4 - 0,267 \over 2} = 0,0665
- pole przekroju
A_1 = {\pi \cdot D_w^2 \over 4} = {3,12 \cdot 0,267^2 \over 4} = 0,05599
- początkowa objętość elementu
V_{01} = A_1 \cdot L_1 = 0,05599 \cdot 1000 = 22,99
- współczynnik A/L/ρ w równaniu ruchu
{dQ \over dt} = {A \over L \cdot \rho} \cdot \left ( p_1 - p_2 - p_t - p_g \right ) (1)
{A_1 \over L_1 \cdot \rho } = {0,05599 \over 1000 \cdot 1000} = 5,599E-08
- wysokość ciśnienia dla elementu
H_{g1} = Rz_{1.2} - Rz_{1.1} = 50 - 0 = 50
- ciśnienie wywołane ciężarem elementu
p_{g1}=H_{g1} \cdot \rho \cdot g=50 \cdot 1000 \cdot 9,81=4905000
- rezystancje rurociągu
R_p1 = {8 \cdot \rho \over \pi^2 \cdot D_{w1}^4} \left ( \lambda \cdot {L_1 \over D_{w1}} + \zeta \right ) = {8 \cdot 1000 \over 3,14^2 \cdot 0,267^4} \cdot \left( 0,02 \cdot {1000 \over 0,267} + 0 \right) = 11947139
- początkowe ciśnienie strat
p_{s1}=R_{p1} \cdot Q^2= 11947139 \cdot 0,1389^2=230462
- ciśnienie początkowe przed elementem
p_{5}=p_{g5} + p_{s5}
p_{4}=p_5 + p_{g4} + p_{s4}
p_{3}=p_4 + p_{g3} + p_{s3}
p_{2}=p_3 + p_{g2} + p_{s2}
p_{1}=p_2 + p_{g1} + p_{s1} = 3092794
- odwrotność współczynnika sprężystości objętościowej elementu
p_1 = {1 \over k_o} \cdot \Delta V
k_{o.1}= {1 \over V_{0.1} \cdot \left ( {D_{w1} \over E_r \cdot e_1} + {1 \over E_c} \right ) } = {1 \over 55,99 \cdot \left ( {0,267 \over 3,2E+9 \cdot 0,0665 } + {1 \over 20,3E+9} \right ) } = 10221570
- początkowa zmiana objętości elementu
\Delta V_1 = {p_{1.1} \over {1 \over k_{o.1}}}={3092794 \over 10221570} = 0,3026
Stałe i wartości początkowe w równaniach elementów rurociągu zebrano w tab.3.
Tab.3. Współczynniki i wartości początkowe elementów rurociągu

3. Obliczenia symulacyjne
Obliczenia symulacyjne przeprowadzimy poprzez całkowanie równania ruchu. Prosty sposób całkowania, z wykorzystaniem arkusza kalkulacyjnego, opisałem na stronie całkowanie równania ruchu cieczy. Odnośniki do arkuszy, z przykładem obliczeniowym, znajdują się na końcu strony.
Do symulacji przyjmuję krok całowania dt = 0.05s.
W czasie pierwszych 10-ciu kroków układ jest w równowadze, a przepływ wynosi Q = 500 m3/h. Po tym czasie przepływ skokowo spada do zera, co dopowiada awaryjnemu wyłączeniu pomp.
W arkuszu ciśnienie strat, z zachowaniem zwrotu, obliczane jest na podstawie przepływu w elemencie i jego rezystancji, na przykład:
p_{1 str} = R_p \cdot abs(Q_1) \cdot Q_1
Ciśnienie między elementami obliczane jest na podstawie różnicy objętości cieczy, która przepłynęła przez sąsiadujące elementy i odwrotności współczynnika sprężystości elementu. Ciśnienie to nie może spaść poniżej ciśnienia parowania cieczy, stąd ograniczenia, jak w przykładzie:
p1 = max \left ( p_{min} ; {1 \over k_{o.1}} \cdot \left (V_0 - V_1 \right ) \right )
Fragment arkusza kalkulacyjnego pokazano na rys.3.
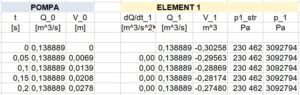
Rys.3. Całkowanie równań ruchu
W załączonym arkuszu kalkulacyjnym obliczenia przeprowadzono dla 600 kroków całkowania, co daje czas symulacji t=30s.
4. Analiza wyników obliczeń
Obliczenia symulacyjne prowadzimy w podstawowych jednostkach SI, które nie zawsze są wygodne w interpretacji wyników. Uzyskane wartości przepływu i ciśnienia można zamienić na jednostki powszechnie stosowane w pomiarach i zestawić w formie wygodnej do tworzenia wykresów, co pokazano na rys.4.
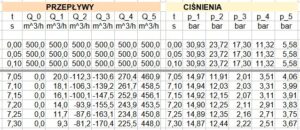
Rys.4. Zestawienie wyników symulacji
Uzyskane przebiegi przepływu i ciśnienia w czasie pokazano na rysunkach 4 i 5.
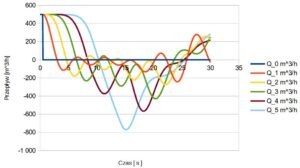
Rys.4. Zmiana przepływu w rurociąg
- Z wykresu 4 wynika, że czas reakcji ostatniego elementu na, skokową zmianę przepływu (wyłączenie pompy) wynosi ok. 5s.
- Maksymalny przepływ powrotny występuje po ok. 15s w końcowej części rurociągu i jego wartość jest znacznie większa niż przepływ wymuszony przez pompę.
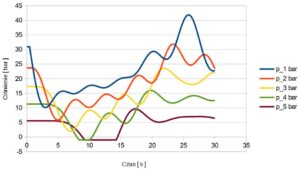
Rys.5. Ciśnienie na początku każdego z odcinków rurociągu
- Dla odcinka 4 i 5 ciśnienie w rurociągu osiąga ciśnienie prężności par (pozioma część wykresu ciśnienia).
- Maksymalne ciśnienie na początku rurociągu wystąpi po ok. 25s.
- Maksymalne ciśnienie na początku rurociągu przekracza o 10 bar ciśnienie nominalne rury P1 = 42 > PN32.
- Maksymalne ciśnienie na początku drugiego docinka rurociągu również przekracza ciśnienie nominalne rury P2 = 32 > PN 25.
- Maksymalne ciśnienie na początku trzeciego docinka przekracza o 4 bary nominalne ciśnienie rury P3 = 29 > PN25.
Z przeprowadzonych symulacji wynika, że konieczne jest zabezpieczenie rurociąg przed nadmiernym wzrostem ciśnienia na pierwszych trzech odcinkach rurociągu.
5. Obliczenia symulacyjne z wykorzystaniem programu Simulink
Dane wejściowe do symulacji umieszczono w pliku wsadowym, którego fragment pokazuje rys.6.
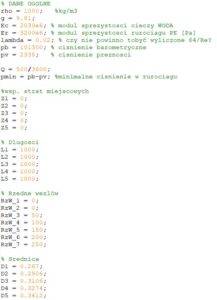
Rys.6. Plik wsadowy z parametrami układu
Obliczenia zrealizowano w programie do symulacji procesów dynamicznych Mathlab-Simulink. Na rys. 7 pokazano fragment schematu, na którym widoczne są bloki obliczeniowe, od lewej: pompy, elementu 1 i elementu 2.
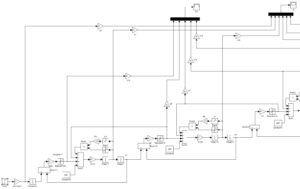
Rys.7. Schemat blokowy do symulacji uderzenia hydraulicznego
Wyniki obliczeń symulacyjnych przedstawiono na rys. 8 i 9.
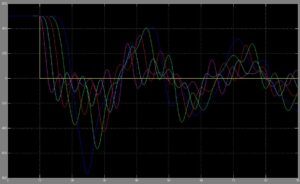
Rys.8. Zmiana przepływu w rurociąg
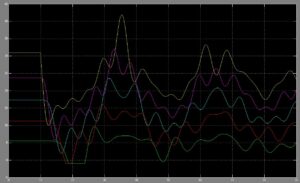
Rys.9. Ciśnienie na początku każdego z odcinków rurociągu
Z analizy wykresów na rysunkach 8 i 9 wynika, że oscylacje przepływu i ciśnienia w rurociągu mają charakter gasnący i zanikają po ok. 10 min.
PLIKI DO POBRANIA
- Arkusz kalkulacyjny: UderzenieHydrauliczne.ods
- Arkusz kalkulacyjny: UderzenieHydrauliczne.xlsx
- Plik wsadowy: UderzenieHydrauliczneDane.m
- Model blokowy Simulink: UderzenieHydrauliczneModel.mdl
PAMIĘTAJ
- Opis uderzenia hydraulicznego, za pomocą analogii kolejowej, nie jest dokładny
- Krok całkowania należy dostosować do prędkości zmian parametrów
- Czas całkowania, w arkuszu kalkulacyjnym, można wydłużyć przez wielokrotne kopiowanie ostatniego wiersza
- W analizowanym przykładzie, wyniki symulacji w arkuszy kalkulacyjnym i programie Simulink nie wykazują istotnych różnic
- O tym, czy wyniki obliczeń dobrze opisują zjawisko, w większym stopniu decyduje wiedza inżyniera, niż koszt użytego oprogramowania.
Warto sprawdzić:
