W tym rozdziale wykorzystam prostą metodę całkowania równań różniczkowych do obliczenia rozruchu układu pompowego (obliczenia równań ruchu).
(Bez paniki, nie zamykaj strony, to banalnie proste)
Najprostszą metodą całkowania numerycznego (obliczania pola powierzchni pod krzywą) jest metoda prostokątów (metoda Newtona).
Klasyczna metoda prostokątów zakłada wyznaczenie wartości funkcji w środku kroku całkowania.
Moim celem jest jak najprostsze wyjaśnienie zjawisk dynamicznych występujących w układach pompowych, stąd, w przykładach obliczeniowych wykorzystuję Excell’a i jeszcze prostszą metodę wykorzystującą wartość funkcji z poprzedniego kroku całkowania, jak to pokazano na rys.1.
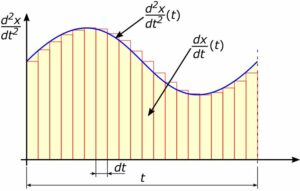
Rys. 1. Całkowanie „uproszczoną” metodą prostokątów
Takie podejście do obliczeń dynamicznych zapewnia wystarczającą dokładność do wyjaśnienia zmian parametrów układów w czasie.
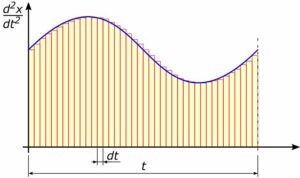
Rys. 2. Zmniejszenie kroku całkowania w celu zwiększenia dokładności obliczeń
Jeżeli zajdzie potrzeba zwiększenia dokładności, w prosty sposób będziesz mógł(a) skopiować formuły Exell’a do dowolnej liczby wierszy i dowolnie zmniejszyć krok całkowania.
Rozpatrzmy przykład pracy rurociągu
Rurociąg jest poziomy.
Pompa na stałą wysokość podnoszenia.
Parametry rurociągu Qn = 1 m3/s - obliczeniowy przepływ w rurociągu ΔHn = 100 m - obliczeniowe straty w rurociągu Hp = 80 m - wysokość podnoszenia pompy d = 1 m - średnica rury L = 5000 m - długość rury ρ = 1000 kg/m3 - gęstość cieczy (woda)
Obliczamy:
- pole przekroju rury A ze znanego wzoru:
A = {\pi \cdot d^2 \over 4} (1)
- masę cieczy m ze wzoru:
m = A \cdot L \cdot \rho (2)
- opory rurociągu określa rezystancja wyznaczona ze wzoru:
R = {H_n \over Q_n^2} (3)
- oraz siłę działającą na ciecz jako:
F = (H_p - H_u) \cdot \rho \cdot g \cdot A = (H_p - R \cdot Q^2) \cdot \rho \cdot g \cdot A (4)
Zakładam, że w momencie startu, dla czasu t=0, ciecz jest w bezruchu. Oznacza to, że:
- droga w czasie t=0 jest równe 0
x_0 = 0 (5)
- prędkość w czasie t=0 jest równe 0
({dx \over dt})_0 = 0 (6)
- przyśpieszenie w czasie t=0 obliczamy na podstawie równania ruchu
({d^2x \over dt^2})_0 = {F_0 \over m} (7)
W czasie t=0 uruchamiamy pompę obciążoną stałym ciśnieniu Hp. W zerowym kroku całkowania, przy zerowej prędkości przepływu, na ciecz będzie działała siła:
F_0 = H_p \cdot \rho \cdot g \cdot A (8)
Przyśpieszenie w następnym kroku całkowania będzie wynikało z siły działającej na ciecz w poprzednim kroku:
({d^2x \over dt^2})_{n+1} = {F_n \over m} (9)
a prędkość i przemieszczenie będą wynosiły odpowiednio:
({dx \over dt})_{n+1} = ({dx \over dt})_n + ({d^2x \over dt^2})_{n+1} \cdot dt (10)
(x)_{n+1} = (x)_n + ({dx \over dt})_{n+1} \cdot dt (11)
Zapis arkusza kalkulacyjnego dla 100 kroków obliczeniowych przedstawia rys. 3.
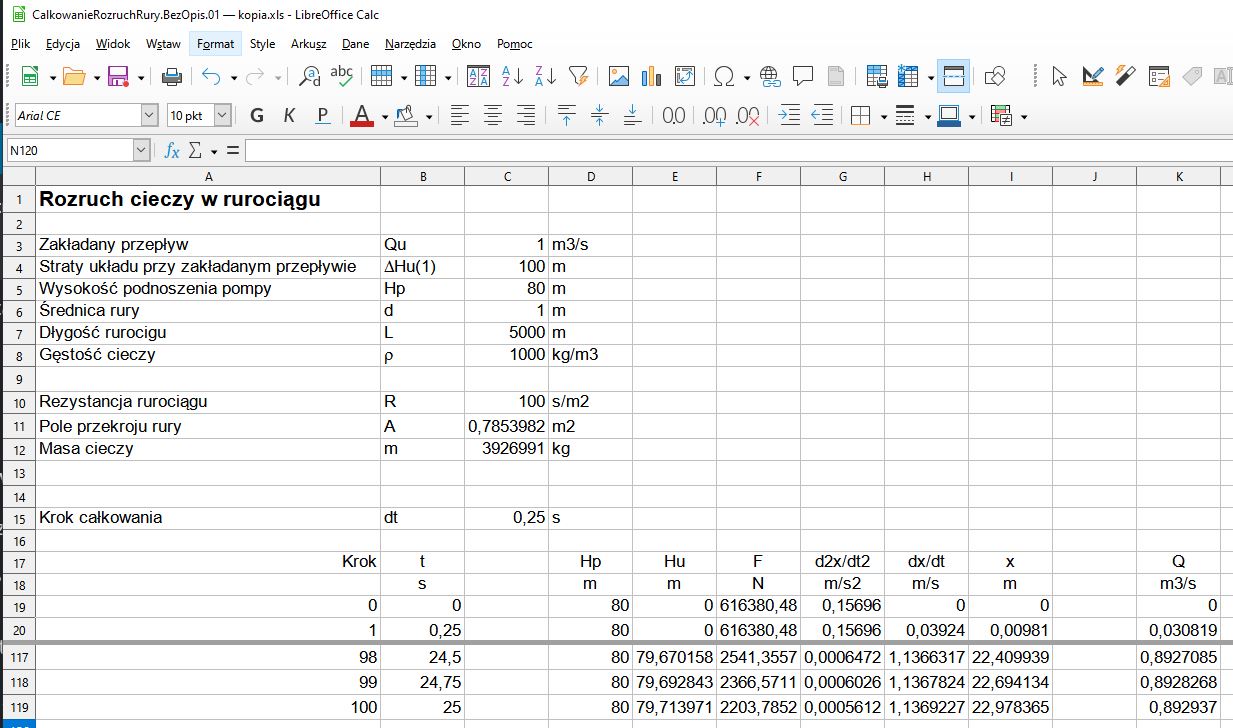
Rys. 3. Przykład obliczeń rozruchu cieczy w rurociągu
Zawartość komórek arkusza obliczeniowego pokazano na rys. 4.
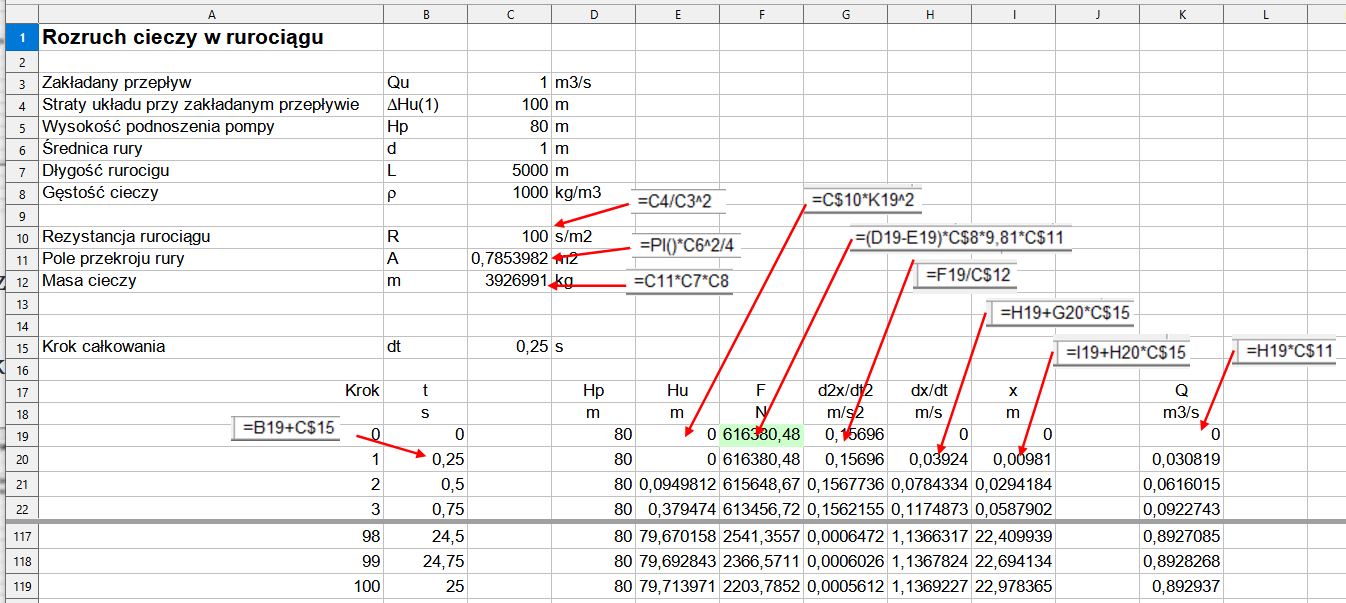
Rys. 4. Algorytm obliczeń parametrów rozruchu cieczy
Obliczenia przeprowadzono dla kroku całkowania dt =0,25 s.
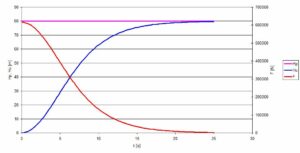Rys. 5. Siła działająca na ciecz w zależności od czasu
Na rys. 5 fioletowa pozioma linia reprezentuje stałą wysokość podnoszenia pompy. Linia niebieska opory przepływu w rurociągu, a linia czerwona niezrównoważoną siłę działającą na ciecz. Jak wynika z wykresu po ok. 25s wysokość oporów rurociągu wyrównuje się z wysokością ciśnienia pompy.
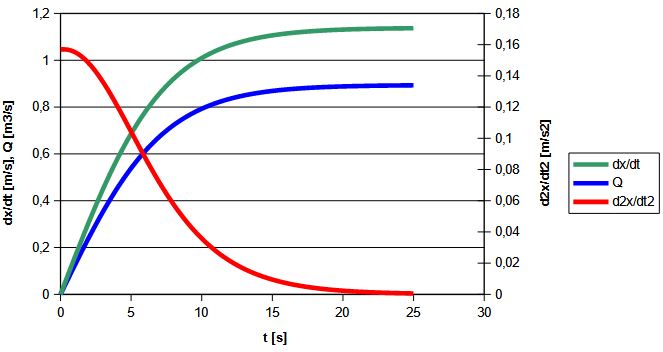
Rys. 6. Przepływ w rurociągu w zależności od czasu
Na rys. 6 czerwona linia reprezentuje przyśpieszenie cieczy. Widoczny jest skokowy wzrost przyśpieszenia w czasie pierwszego kroku obliczeniowego.
Linia zielona i niebieska reprezentują prędkość i przepływ cieczy. Widzimy, że przepływ stabilizuje się po ok. 25s.
Sprawdź wpływ kroku całkowania na wynik obliczeń
PAMIĘTAJ !
- Całkowanie metodą prostokątów (nawet uproszczoną) skutecznie pozwala na obliczenie większości zagadnień inżynierskich
- Możesz wykorzystać arkusz kalkulacyjny do obliczeń dynamicznych
- Sprawdź wpływ kroku całkowania na dokładność wyników obliczeń
- W obliczeniach pominięto zjawiska falowe!
Warto sprawdzić: