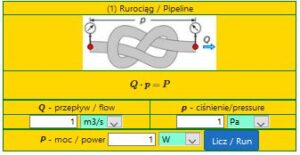
Ile „kosztują” straty? Ile mocy można „zarobić” na mocy hydraulicznej?
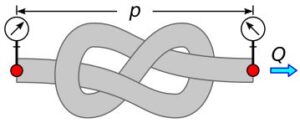
Rys.1. Moc strat w rurociągu
P = Q \cdot p (1)
P - moc strat w rurociągu Q - przepływ p - ciśnienie (tak naprawdę Δp - różnica ciśnienia ma początku i na końcu)
Przypadki zastosowań:
- rury
- węże, wężownice
- wyodrębnione części układu z pojedynczym wlotem i wylotem
Oblicz moc strat pojedynczego rurociągu 
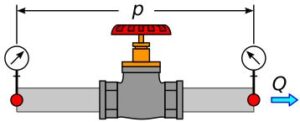
Rys.2. Moc strat zaworu
P = Q \cdot p (2)
P - moc strat w zaworze Q - przepływ p - ciśnienie (Δp, różnica ciśnienia przed i za zaworem)
Przypadki zastosowań:
- zawory, zasuwy, kurki
- kolana, trójniki
- kryzy, zwężenia, rozszerzenia
- kaloryfery, kotły, wymienniki
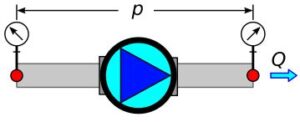
Rys.3. Moc hydrauliczna pompy
P = Q \cdot p (3)
P - moc "dostarczana" do układu Q - przepływ p - ciśnienie (Δp, różnica ciśnienia za i przed pompą)
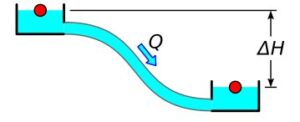
Rys.4. Moc spływu między zbiornikami
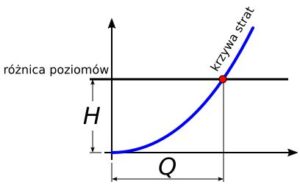
Rys.5. Straty przepływu równe różnicy poziomów
P = Q \cdot H \cdot \rho \cdot g (4)
P - moc spływu między zbiornikami Q - przepływ H - spad (ΔH, różnica rzędnych lustra górnego i dolnego) ρ - gęstość cieczy g - przyśpieszenie ziemskie
Przypadki zastosowań:
- spływ między zbiornikami
- elektrownie, elektrownie szczytowo-pompowe
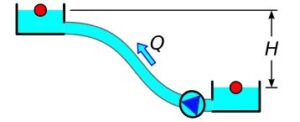
Rys.5. Moc podnoszenia statycznego układu pompowego
P = Q \cdot H \cdot \rho \cdot g (5)
Uwaga! W równaniu 5 pominięto straty w rurociągów.
P - moc hydrauliczna podnoszenia statycznego Q - wydajność pompy H - geometryczna wysokość podnoszenia (ΔH, różnica rzędnych lustra górnego i dolnego) ρ - gęstość cieczy g - przyśpieszenie ziemskie
Przypadki zastosowań:
- układy pompowe
- elektrownie szczytowo-pompowe
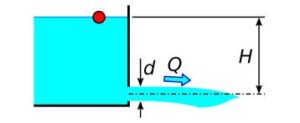
Rys.6. Moc strat wypływu grawitacyjnego ze zbiornika
Wypływ
Q = \mu \cdot A \cdot \sqrt{2 \cdot g \cdot H} (6)
Na podstawie wzorów 4 i 6 moc wypływu określa wzór 7.
P = Q\cdot H \cdot \rho \cdot g = \mu \cdot A \cdot \sqrt{2 \cdot g \cdot H} \cdot H \cdot \rho \cdot g (7)
Przyjmuję średni współczynnik wypływu wg. Hydraulika J.Sobota.
\mu = 0,65 (8)
Ostatecznie dla otworu kołowego o średnicy d moc wypływu określa wzór 9.
P = 0,65 \cdot \sqrt{2} \cdot {\pi \cdot d^2 \over 4} \cdot H^{3 \over 2} \cdot g^{3 \over 2} \cdot \rho (9)
P - moc hydrauliczna wypływu Q - wypływ H - wysokość (ΔH, różnica rzędnych lustra i otworu) d - średnica otworu μ - współczynnik wydatku ρ - gęstość cieczy g - przyśpieszenie ziemskie
Przypadki zastosowań:
- wypływ przez otwory
- przecieki
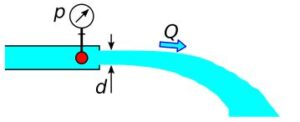
Rys.7. Moc wypływu pod ciśnieniem
Wypływ z otworu
Q = \mu \cdot A \cdot \sqrt{2 \cdot p \over \rho} (10)
Przyjmuję współczynnik wypływu dla dużych otworów wg. Hydraulika J.Sobota.
\mu = 0,7 (11)
Ostatecznie na podstawie wzorów 1, 10 i 11 dla otworu kołowego o średnicy d moc wypływu określa wzór 12.
P = 0,7 \cdot {\pi \cdot d^2 \over 4} \cdot \sqrt{2 \cdot p \over \rho} \cdot p (12)
P - moc hydrauliczna wypływu Q - wypływ p - ciśnienie d - średnica otworu μ - współczynnik wydatku ρ - gęstość cieczy g - przyśpieszenie ziemskie
Przypadki zastosowań:
- wypływ z rury
- wypływ z zaworu czerpalnego,
- wypływ z kranu (np. do wanny)
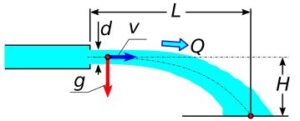
Rys.8. Moc wypływu swobodny nad powierzchnią
Prędkość rzeczywista w kierunku poziomym v określa wzór 13.
v = {L \over t} (13)
Przyśpieszenie w kierunku pionowym g określa wzór 14.
g = {2 \cdot H \over t^2} (14)
Na podstawie wzorów 13 i 14 po wyrugowaniu czasu t prędkość cieczy v określa wzór 15.
v = {\sqrt{g \over 2} \cdot {L \over \sqrt{H}}} (15)
Przepływ dla otworu kołowego o średnicy d określa wzór 16.
Q = {\pi \cdot d^2 \over 4} \cdot {\sqrt{g \over 2} \cdot {L \over \sqrt{H}}} (16)
Ostatecznie na podstawie wzorów 4 i 16 moc wypływu określa wzór 17.
P = {\pi \cdot d^2 \over 4 \cdot \sqrt{2}} \cdot L \cdot \sqrt{H} \cdot \rho \cdot g^{3 \over 2} (17)
P - moc hydrauliczna wypływu Q - wypływ L - zasięg strumienia H - wysokość nad poziom odniesienia d - średnica strumienia v - prędkość cieczy (prędkość średnia) t - czas przemieszczania się cieczy między wylotem a poziomem odniesienia ρ - gęstość cieczy g - przyśpieszenie ziemskie
Przypadki zastosowań:
- sikawka
- wypływ z rury
- wypływ ze zbiornika
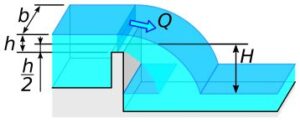
Rys.9. Moc przelewu nieztopionego (prostokątnego)
Na podstawie wzoru 6 przepływ przez przelew opisuje równanie 18.
Q = \mu \cdot h \cdot b \cdot \sqrt{2 \cdot g \cdot h} (18)
Przyjmuję współczynnik wypływu dla typowego przelewu prostokątnego wg. Hydraulika J.Sobota.
\mu = 0,49 (19)
Ostatecznie na podstawie wzorów 4, 18 i 19 moc przelewu określa wzór 20.
P = 0,49 \cdot \sqrt{2} \cdot b \cdot g^{3 \over 2} \cdot h^{3 \over 2} \cdot H \cdot \rho (20)
P - moc hydrauliczna przelewu niezatopionego Q - przepływ h - wysokość nad progiem H - wysokość nad lustrem dolnej wody b - szerokość przelewu ρ - gęstość cieczy g - przyśpieszenie ziemskie
Przypadki zastosowań:
- jazy, zastawki
- wypływy z pompowni
- wypływy z elektrowni
Rys.10. Kinetyczna moc przepływu
Na podstawie wzoru Toroczellego wysokość energii kinetycznej przepływu opisuje wzór 21.
H = {v^2 \over 2 \cdot g} (21)
Na podstawie równania ciągłości przepływ Q opisuje równanie 22.
Q = A \cdot v = {\pi \cdot d^2 \over 4} \cdot v (22)
Ostatecznie na podstawie wzorów 4, 21 i 22 moc kinetyczną przepływu określa wzór 23.
P = {\pi \cdot d^2 \over 8} \cdot v^3 \cdot \rho (23)
P - moc kinetyczna przelewu v - prędkość Q - przepływ H - wysokość energii kinetycznej, wysokość energii prędkości ρ - gęstość cieczy
Przypadki zastosowań:
- turbiny hydrokinetyczne
- wiatraki
PAMIĘTAJ
- Moc P razy czas t to energia E, a energia E razy cena jednostkowa energii cj (np. 60gr/kWh) to zysk albo strata, P \cdot t \cdot c_j = zysk/strata
- Przy szacowaniu strat dolicz sprawność pompy i silnika
- Przy szacowaniu zysków odlicz sprawność turbiny i generatora
- Opisane przypadki obliczeń mocy hydraulicznej zostały opracowane do szacowania zasobów energetycznych i budowy podręcznego Kalkulatora Mocy
- Błąd oszacowania mocy może wynosić kilka lub nawet kilkanaście procent
- Aby zwiększyć dokładność – sprawdź wartości współczynników wydatku
WARTO SPRAWDZIĆ: