1. Szkieletowa łopatki 2D
W metodzie punktowej 2D kształt szkieletowej łopatki, jak sama nazwa wskazuje, jest opisana zbiorem punktów. Położenie tych punktów, we współrzędnych biegunowych, określają: promień r i kąt θ jak to pokazano na rys.1. Współrzędna r zmienia się od wartości r1 – promień wlotowy, do wartości r2 – promień wylotowy. 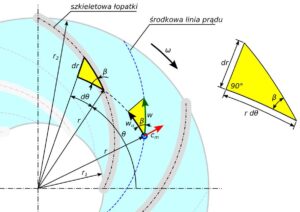
Rys.1. Kąt łopatki i zarys szkieletowej we współrzędnych biegunowych.
Zgodnie z teorią Eulera, dla nieskończonej liczby nieskończenie cienkich łopatek, środkowa linia prądu pokrywa się ze szkieletową łopatki. W przypadku obliczeń dla skończonej liczby zakładamy, że środkowa linia prądu, z wystarczającą dokładnością, także pokrywa się ze szkieletową łopatki.
Tangens kąta łopatki, patrz rys.1, dla dowolnego promienia r opisany jest równaniem 1.
tg \ \beta = {dr \over r \cdot d \theta} (1)
β - kąt szkieletowej łopatki r - promień dr - przyrost promienia θ - współrzędna kątowa dθ - przyrost współrzędnej kątowej r·dθ - przyrost długości łuku
Po przekształceniu równania 1 przyrost współrzędnej kątowej dθ przy zmianie promienia o dr opisuje wzór 2.
d \theta = {1 \over r \cdot tg \ \beta} \cdot dr (2)
Współrzędną kątową obliczamy poprzez całkowanie przyrostów współrzędnej kątowej od początku łopatki, od promienia r1, do wybranego promienia r, na podstawie wzoru 3.
\theta = \int_{r_1}^r {1 \over r \cdot tg \ \beta} \cdot dr (3)
Przy liczbie punktów 10 lub więcej, całkowanie z wystarczającą dokładnością można zastąpić sumowaniem zgodnie ze wzorem 4.
\theta = \Sigma_{r_1}^r {1 \over r \cdot tg \ \beta} \cdot \Delta r (4)
2. Współczynnik przesłonięcia przekroju
Pole powierzchni przepływowej netto – powierzchnia bez łopatek, patrz rys. 2 , obliczamy ze wzoru 5.
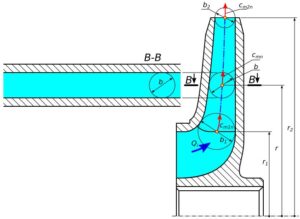
Rys.2. Pole przekroju przepływowego netto – bez łopatek
A_n = 2 \cdot \pi \cdot r \cdot b (5)
Łopatki o określonej grubości, wynikającej z wymagań technologicznych i wytrzymałościowych, ograniczają pole powierzchni przepływowej wirnika. Sposób obliczania rzutu grubości łopatki na kierunek unoszenia su, pokazuje rys 3.
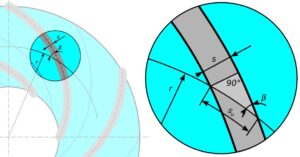
Rys.3. Rzut grubości łopatki
Rzut grubości łopatki na kierunek unoszenia obliczamy ze wzoru 6.
s_u = {S \over sin \ \beta} (6)
b - szerokość wirnika b1 - szerokość wirnika na wlocie b2 - szerokość wirnika na wylocie A - pole powierzchni przepływowej An - pole powierzchni przepływowej netto s - grubość łopatki su - rzut grubości łopatki na kierunek unoszenia Z - liczba łopatek φ - współczynnik przesłonięcia przekroju przepływowego t - podziałka
Pole rzeczywistej powierzchni przepływowej – powierzchnia po uwzględnieniu grubości łopatek, patrz rys. 4, obliczamy ze wzoru 7.
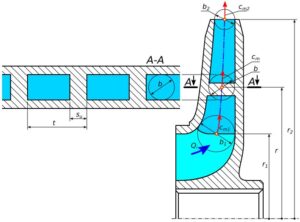
Rys.4. Rzeczywiste pole przekroju przepływowego z uwzględnieniem grubości łopatek
A = \left( 2 \cdot \pi \cdot r - Z\cdot s_u \right) \cdot b (7)
Podziałkę wirnika dla wybranego promienia obliczamy ze wzoru 8.
t = {2 \cdot \pi \cdot r \over Z} (8)
Współczynnik przesłonięcia przekroju przepływowego jest zdefiniowany jako stosunek pola powierzchni przepływowej netto An do rzeczywistej powierzchni przepływowej A , wzór 9.
\varphi = {A_n \over A} (9)
Do wzoru definicyjnego 9 wstawiamy wzory 5 i 7 oraz zależność 8.
\varphi = {2 \cdot \pi \cdot r \cdot b \over \left( 2 \cdot \pi \cdot r - Z\cdot s_u \right) \cdot b} = {{2 \cdot \pi \cdot r \over Z} \over {2 \cdot \pi \cdot r \over Z} - s_u } = {t \over t - s_u } (10)
Ostatecznie po podstawieniu do wzoru 10 zależności 6 otrzymamy wzór na współczynnik przesłonięcia przekroju 11.
\varphi = {t \over t - {s \over sin \ \beta}} (11)
3. Obliczenia prędkości merydionalnej
Na podstawie równania ciągłości, dla powierzchni An, prędkość merydionalna netto cmn jest opisana równaniem 12.
c_{mn} = {Q_i \over A_n} (12)
W podobny sposób, dla powierzchni A, prędkość merydionalna cm opisuje równanie 13.
c_m = {Q_i \over A} (13)
Qi - przepływ wewnętrzny cm - prędkość merydionalna cmn - prędkość merydionalna netto w - prędkość względna wu - rzut prędkości względnej na kierunek prędkości unoszenia
Po podstawieniu do równania 9 wartości A i An z zależności 12 i 13 otrzymamy związek między współczynnikiem przesłonięcia φ a prędkościami merydionalnymi cm i cmn.
\varphi = {Q_i \cdot c_m \over Q_i \cdot c_{mn}} = {c_m \over c_{mn}} (14)
4. Obliczenia kąta łopatki
Przez podstawienie wyrażenia 11 do 14 eliminujemy współczynnik przesłonięcia przekroju φ i otrzymujemy związek 15.
{c_m \over c_{mn}} = {t \over t - {s \over sin \ \beta}} (15)
W pierwszym kroku, mnożymy równanie 15 stronami.
t - {s \over sin \ \beta} = {t \cdot c_{mn} \over c_m}
Następnie obie stront mnożymy przez sin β i dzielimy prze t.
sin \ \beta - {s \over t} = {c_{mn} \cdot sin \ \beta \over c_m} (16)
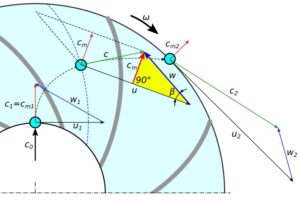
Rys.5. Trójkąt prędkości cieczy
Na podstawie założenia, że środkowa linia prądu, pokrywa się ze szkieletową łopatki, porównaj rysunki 1 i 6, prędkość merydionalną cm możemy obliczyć z równania 17.
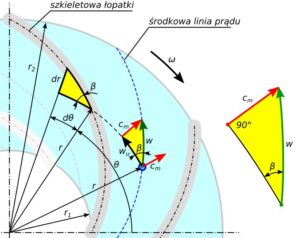
Rys.5. Zależność prędkości merydionalnej i prędkości względnej od kąta łopatki
c_m = w \cdot sin \ \beta (17)
Po podstawieniu równania 17 do 16 i uporządkowaniu stron otrzymamy proste równanie 18, określające kat łopatki β (sin β) w zależności od prędkości merydionalnej netto i prędkości względnej, z poprawką uwzględniającą grubość łopatki.
sin \ \beta = {c_{mn} \over w} + {s \over t} (18)
5. Kształtowanie szkieletowej łopatki
Obliczenia kształtu szkieletowej łopatki prowadzone są tabelarycznie, np. w arkuszu kalkulacyjnym Calc lub Excel.
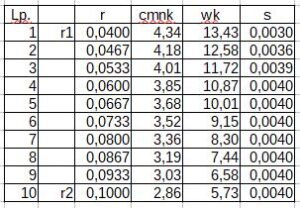
Tab. 1. Dane do obliczeń
W obliczaniach kształtu szkieletowej łopatki, aby uwzględnić kąt natarcia, wykorzystujemy konstrukcyjny kąt łopatki β1k
cmnk1 - prędkość merydionalna netto dla kąta konstrukcyjnego β1k (z trójkąta na wlocie) wk1 - prędkość względna dla kąta konstrukcyjnego β1k (z trójkąta na wlocie)
W kolumnie r umieszczona jest wartość promienia punktu obliczeniowego. W wierszu 1 i 10 umieszczone są odpowiednio promień wlotowy i wylotowy. W kolumnie cmnk, w odpowiednich wierszach, znajdują się wartości konstrukcyjnej prędkości merydionalnej netto, w kolumnie wk, znajdują się wartości prędkości względnej, a w kolumnie s, wartości grubości łopatki.
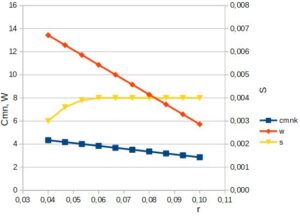
Rys. 6. Zmiana wartości: prędkości merydionalnej netto, prędkości względnej oraz grubości łopatki w zależności od promienia
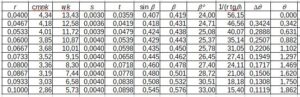
Tab. 2. Obliczenia kąta i współrzędnej kątowej szkieletowej łopatki
Wartości sinusa kąta łopatki i kąta łopatki w kolumnach sinβ i β oraz kąta w stopniach w kolumnie β° są obliczone ze wzoru 18.
Wartości współrzędnej kątowej punktów szkieletowej θ są obliczone ze wzoru 4.
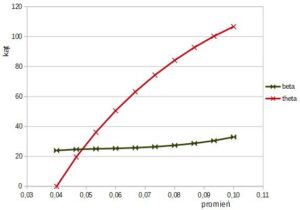
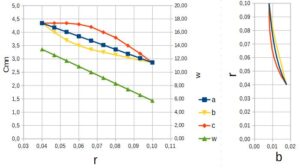
Rys. 7. Zmiana kąta łopatki i współrzędnej kątowej w zależności od promienia
Na rys.7 pokazano jak zmieniają się wartości kąta łopatki β i współrzędnej kątowej θ, przy liniowej zmianie prędkości merydionalnej netto cmn i względnej w.
Zmiany wartości prędkości względnej w rzutują na kształt szkieletowej łopatki. Przykłady trzech przebiegów zmian prędkości względnej i odpowiadające im zmiany szkieletowej łopatki, przy liniowej zmianie prędkości merydionalnej, pokazano na rys. 7 i 8.
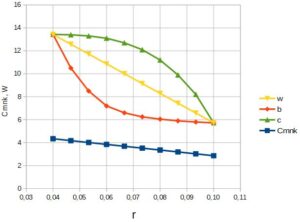
Rys. 7. Zmiana prędkości względnej w funkcji promienia, a – zmiana liniowa, b – duży spadek na początku, c – mały spadek na początku
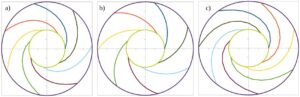
Rys. 8. Kształt szkieletowej łopatki w zależności od przebiegu zmian prędkości względnej w, przy liniowej zmianie prędkości merydionalnej cmn, , a – zmiana liniowa, b – duży spadek na początku, c – mały spadek na początku
Duży spadek prędkości względnej przy mniejszych promieniach – krzywa b na rys. 7, powoduje skrócenia kanału międzyłopatkowego wirnika, rys. 8. b.
Mały spadek prędkości względnej przy mniejszych promieniach – krzywa c na rys. 7, powoduje wydłużenie kanału międzyłopatkowego wirnika, rys. 8. c.
6. Kształtowanie przekroju merydionalnego
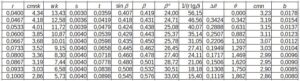
Tab. 3. Obliczenia szerokości wirnika
W przykładzie, w kolumnie cmn, zmiany prędkości merydionalne netto, są obliczone proporcjonalne do zmian prędkości merydionalnej cmnk.
Szerokość wirnika w kolumnie b została obliczona ze wzoru 12 z wykorzystaniem wzoru 5.
Zmiany wartości prędkości cmn rzutują na kształt przekroju merydionalnego wirnika. Przykłady trzech przebiegów zmian prędkości prędkości cmn i dpowiadające im zmiany przekroju merydionalnego, przy liniowej zmianie prędkości względnej, pokazano na rys. 9.
Rys. 9. Kształt przekroju merydionalnego w zależności od przebiegu zmian prędkości merydionalnej cmn, przy liniowej zmianie prędkości względnej w, a – zmiana liniowa, b – duży spadek na początku, c – mały spadek na początku
Duży spadek prędkości merydionalnej przy mniejszych promieniach – krzywa b na rys. 9, powoduje poszerzenie wirnika, a mały spadek prędkości merydionalnej przy mniejszych promieniach – krzywa c na rys. 9, powoduje zwężenie wirnika.
Zmiana przebiegu prędkości merydionalnej w niewielkim stopniu zmienia także zarys łopatki.
PAMIĘTAJ !
- Szkieletowa łopatki i środkowa linia prądu mają taki sam kształt
- Prędkość cm jest składową promieniową prędkości bezwzględnej c
- Prędkość cm i cmn odpowiadają katowi łopatki β
- Prędkość cmk i cmnk odpowiadają katowi konstrukcyjnemu łopatki β
- Zmiana prędkości względnej nie zmienia szerokości wirnika
- Zmiana prędkości względnej zmienia długość łopatki (kąt pokrycia)
- Zmiana prędkości merydionalnej zmienia szerokość wirnika
- Zmiana prędkości merydionalnej zmienia (nieznacznie) długość łopatki
- Łopatka im cieńsza tym lepsza, ograniczeniem jest: wytrzymałość, technologia wykonania oraz zużycie, w przypadku pompowania cieczy silnie ścierających
Warto sprawdzić:
