Zacznijmy od przypomnienia, jak wygląda układ jednomasowy.
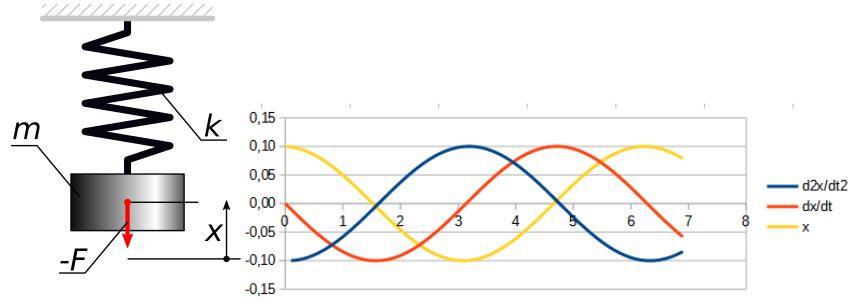
Rys.1. Układ jednomasowy
Częstotliwość i okres drgań własnych układu masa-sprężyna pokazanego na rys. 1 można wyznaczyć ze wzorów 1 i 2, patrz częstotliwość drgań własnych .
f={1 \over 2 \cdot \pi} \cdot \sqrt{k \over m} (1)
T={2 \cdot \pi} \cdot \sqrt{m \over k} (2)
f - częstotliwość T - okres drgań k - współczynnik sprężystości sprężyny m - masa π - liczba pi
Przy założeniu, że m = 1 kg i k = 1 N/m okres drgań dla przypadku pokazanego na rys 1. wynosi T = 6,28s.
Rozważmy trzy przypadki układu trójmasowego pokazane na rys. 2. Wnioski z tych rozważań będzie można zastosować do układów wielomasowych.
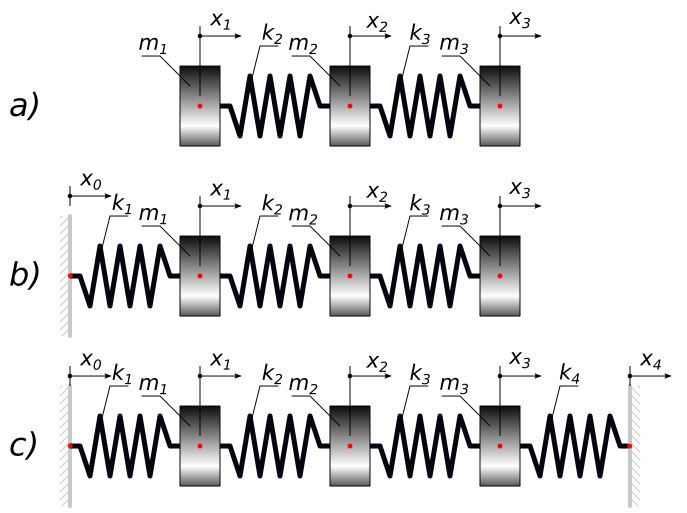
Rys.2. Układy trójmasowe
Równania ruchu mas dla przypadku a) – układ swobodny z obu stron, opisują równania 3 do 5.
m_1 \cdot {d^2x_1 \over dt^2} = k_2 \left( x_2 - x_1 \right) (3)
m_2 \cdot {d^2x_2 \over dt^2} = k_3 \left( x_3 - x_2 \right) - k_2 \left( x_2 - x_1 \right) (4)
m_3 \cdot {d^2x_3 \over dt^2} = - k_3 \left( x_3 - x_2 \right) (5)
Równanie ruchu mas dla przypadku b) – układ utwierdzony z jednej strony, opisują równania 6 do 8.
m_1 \cdot {d^2x_1 \over dt^2} =k_2 \left( x_2 - x_1 \right) - k_1 \left( x_1 - x_0 \right) x_0=0 (6)
m_2 \cdot {d^2x_2 \over dt^2} = k_3 \left( x_3 - x_2 \right) - k_2 \left( x_2 - x_1 \right) (7)
m_3 \cdot {d^2x_3 \over dt^2} = - k_3 \left( x_3 - x_2 \right) (8)
Równanie ruchu mas dla przypadku c) – układ utwierdzony z obu stron, opisują równania 9 do 11.
m_1 \cdot {d^2x_1 \over dt^2} = k_2 \left( x_2 - x_1 \right) - k_1 \left( x_1 - x_0 \right) x_0 = 0 (9)
m_2 \cdot {d^2x_2 \over dt^2} = k_3 \left( x_3 - x_2 \right) - k_2 \left( x_2 - x_1 \right) (10)
m_3 \cdot {d^2x_3 \over dt^2} = k_4 \left( x_4 - x_3 \right) - k_3 \left( x_3 - x_2 \right) x_4=0 (11)
W przypadku gdy masy są równe m1 = m2 = m3 = m i sztywności sprężyn są równe k1 = k2 = k3 = k4 =k, równanie ruchu wybranej masy i opisuje równanie 12.
m \cdot {d^2x_i \over dt^2} = k \left( x_{i+1} - 2 \cdot x_i + x_{i-1} \right) (12)
Zbadajmy wybrane przypadki zachowanie się układów pokazanych na rys. 2, przy różnych wymuszeniach. Do badań wykorzystamy proste symulacje dynamiczne układów w arkuszu kalkulacyjnym.
1. Układ a) przy wymuszeniu przemieszczenia skrajnych mas na początku symulacji o x1(0) = -0,1m i x3(0) = 0,1m.
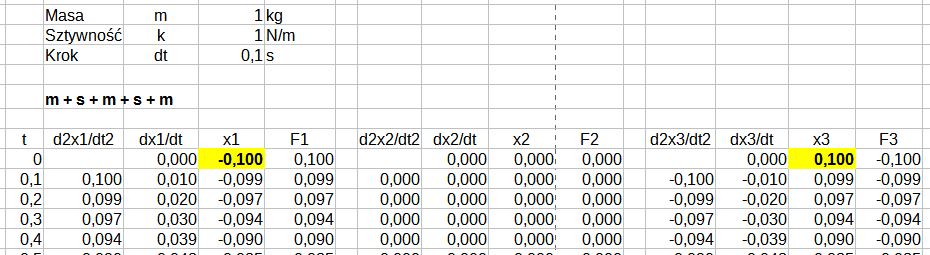
Rys. 3. Symulacja układu a), przemieszczenie masy m1 i m2
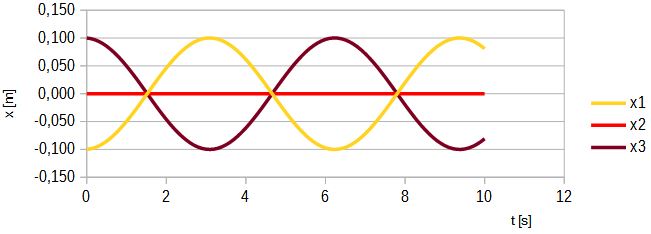
Rys. 4. Przemieszczenia mas dla układu a) przy x1(0) = -0,1 i x3(0) = 0,1
Jak wynika z rys. 4, początkowe przemieszczenie mas skrajnych generuje falę stojącą o okresie T = 6,28s, przy czym masa środkowa pozostaje w spoczynku. Okres ten jest taki sam jak dla układu jednomasowego pokazanego na rys.1. Dla innych wartości m i k częstotliwość i okres można obliczyć ze wzoru 1 i 2.
2. Układ a) przy wymuszeniu przemieszczenia środkowej masy na początku symulacji x2(0) = 0,1m.
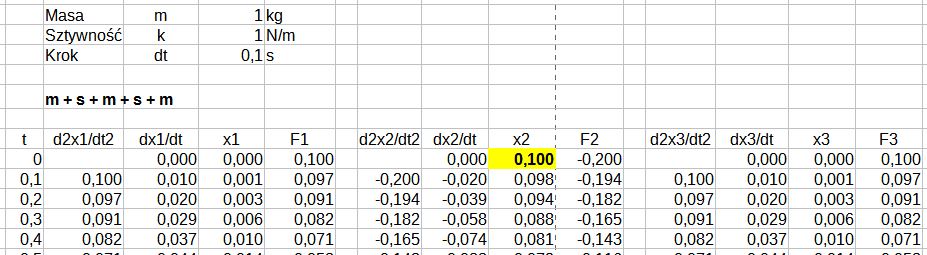
Rys. 5. Symulacja układu a), przemieszczenie masy m2
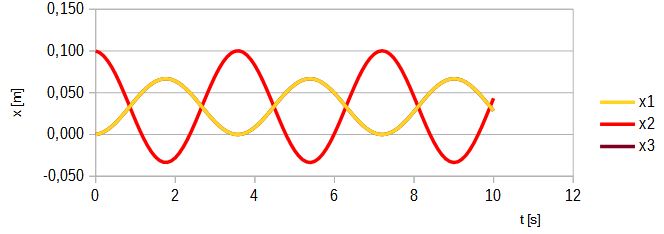 Rys. 6. Przemieszczenia mas dla układu a) przy x2(0) = 0,1
Rys. 6. Przemieszczenia mas dla układu a) przy x2(0) = 0,1
Jak widzimy na rys. 6, początkowe przemieszczenie masy środkowej generuje falę stojącą o okresie T = 3,63s. Dla innych wartości m i k częstotliwość i okres można obliczyć ze wzoru 13 i 14.
f={1 \over 2 \cdot \pi} \cdot \sqrt{3 \cdot k \over m} (13)
T={2 \cdot \pi} \cdot \sqrt{m \over 3 \cdot k} (14)
3. Układ a) przy wymuszeniu przemieszczenia jednej skrajnej masy na początku symulacji o x1(0) = -0,1m.
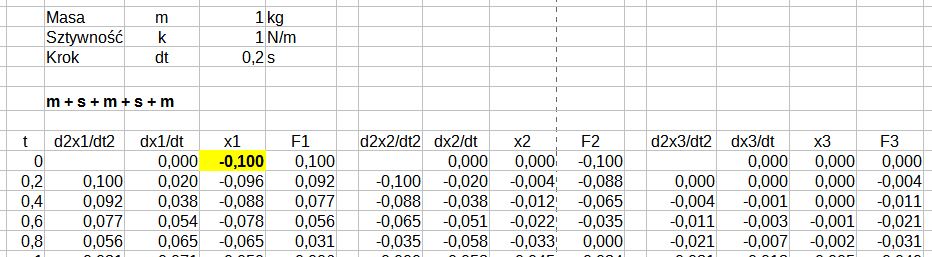
Rys. 7. Symulacja układu a), przemieszczenie masy m1
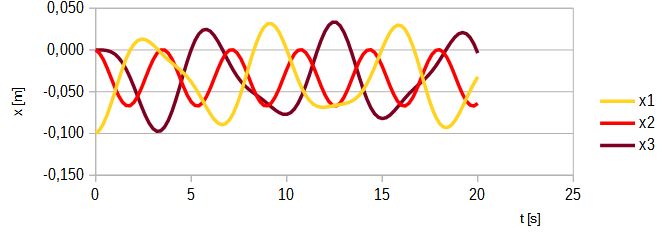 Rys. 8. Przemieszczenia mas dla układu a) przy x1(0) = -0,1
Rys. 8. Przemieszczenia mas dla układu a) przy x1(0) = -0,1
Jak widzimy na rys. 8, początkowe przemieszczenie masy skrajnej generuje fale o okresie około T = 6,28 s dla mas 1 i 3 i T = 3,63 s dla masy 2. Dla innych wartości m i k częstotliwości i okresy tych fal można obliczyć ze wzoru 1, 2 i 13, 14.
4. Układ b) przy wymuszeniu przemieszczenia skrajnych mas na początku symulacji o x1(0) = -0,1m i x3(0) = 0,1m.
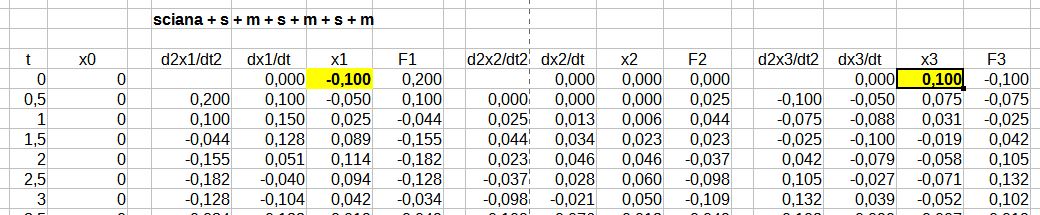
Rys. 9. Symulacja układu b), przemieszczenie masy m1 i m2
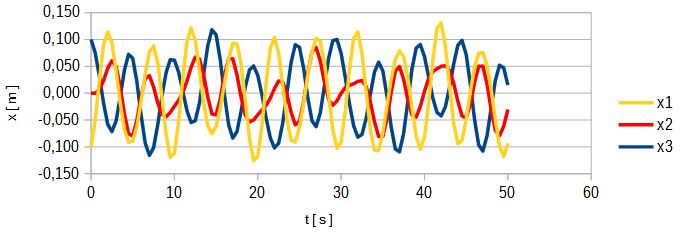 Rys. 10. Przemieszczenia mas dla układu b), x1(0) = -0,1 i x3(0) = 0,1
Rys. 10. Przemieszczenia mas dla układu b), x1(0) = -0,1 i x3(0) = 0,1
Jak wynika z rys. 2b układ jest niesymetryczny. W tym przypadku nawet symetryczne wymuszenie początkowe generuje fale o złożonych kształtach, trudnych do interpretacji.
5. Układ b) przy wymuszeniu przemieszczenia ściany o x0 = 0,1m.
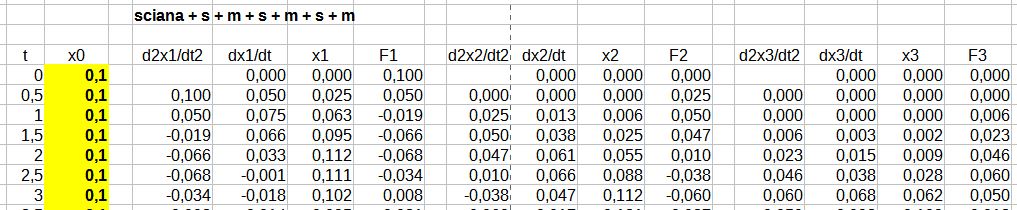
Rys. 11. Symulacja układu b) przy przemieszczeniu ściany
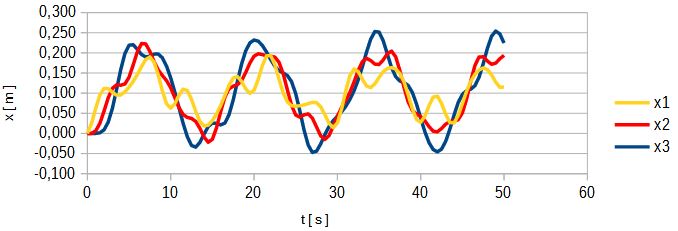
Rys. 12. Przemieszczenia mas dla układu b) po przemieszczeniu ściany
Jak wynika z rys. 12 wymuszenie w postaci przemieszczenia ściany (ściśnięcia sprężyny) generuje fale o różnych okresach drgań nakładających się na siebie. Największą amplitudę ma fala o najdłuższym okresie T = 14,12 s.
Przypadek ten jest bardzo interesujący technicznie ponieważ może być wykorzystany do analiz zachowania się cieczy w otwartych rurociągach tłocznych układów pompowych.
6. Układ c) przy wymuszeniu przemieszczenia skrajnych mas na początku symulacji o x1(0) = -0,1m i x3(0) = 0,1m.
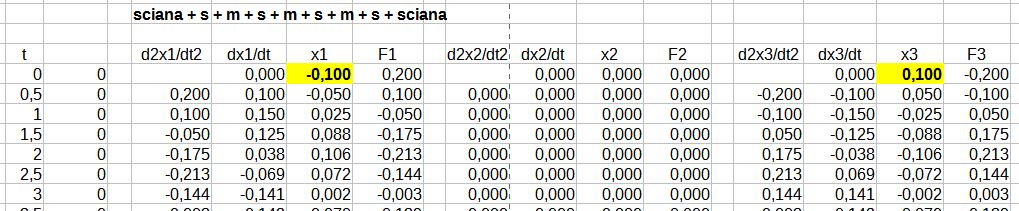
Rys. 13. Symulacja układu c) przy przemieszczeniu masy m1 i m2
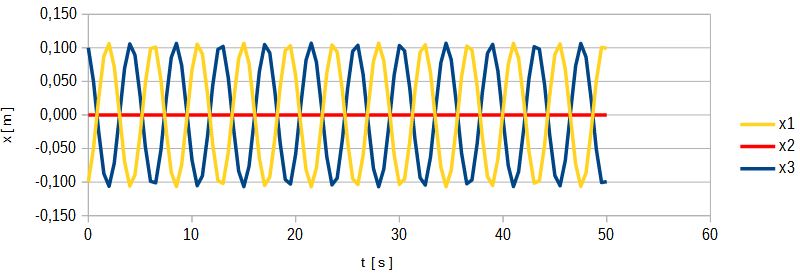 Rys. 14. Przemieszczenia mas dla układu c) po przemieszczeniu skrajnych mas
Rys. 14. Przemieszczenia mas dla układu c) po przemieszczeniu skrajnych mas
Jak wynika z rys. 14, początkowe przemieszczenie mas skrajnych generuje falę stojącą o okresie T = 4,1 s, przy czym masa środkowa pozostaje w spoczynku.
7. Układ c) przy wymuszeniu przemieszczenia ściany o x0 = 0,1m.
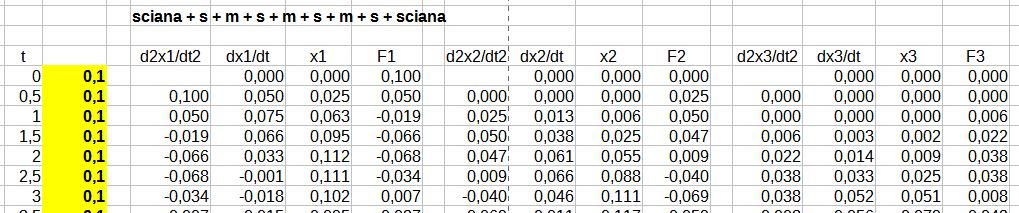
Rys. 15. Symulacja układu c) przy przemieszczeniu ściany
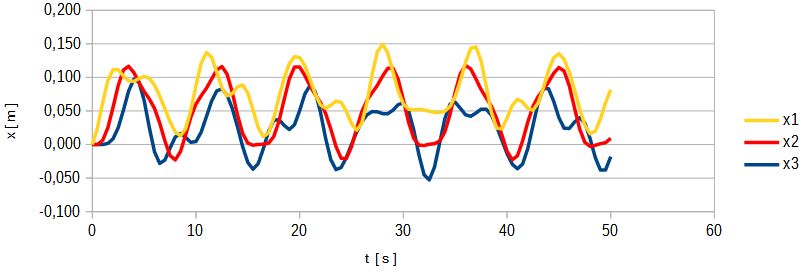
Rys. 16. Przemieszczenia mas dla układu c) po przemieszczeniu ściany
Jak wynika z rys. 16 wymuszenie w postaci przemieszczenia ściany (ściśnięcia sprężyny po lewej) generuje fale o różnych okresach drgań nakładających się na siebie, podobnie jak w punkcie 5. Największą amplitudę ma fala o okresie T = 6,28 s.
Przypadek ten może być wykorzystany do analiz zachowania się cieczy w zamkniętych rurociągach tłocznych układów pompowych.
PAMIĘTAJ !
- Symulacje opisane w punktach 5 i 7 można wykorzystać do analizy dynamicznej układów pompowych,
- Spróbuj samodzielnych symulacji układów dla różnych parametrów z wykorzystaniem arkusza kalkulacyjnego – to proste,
Warto sprawdzić:
