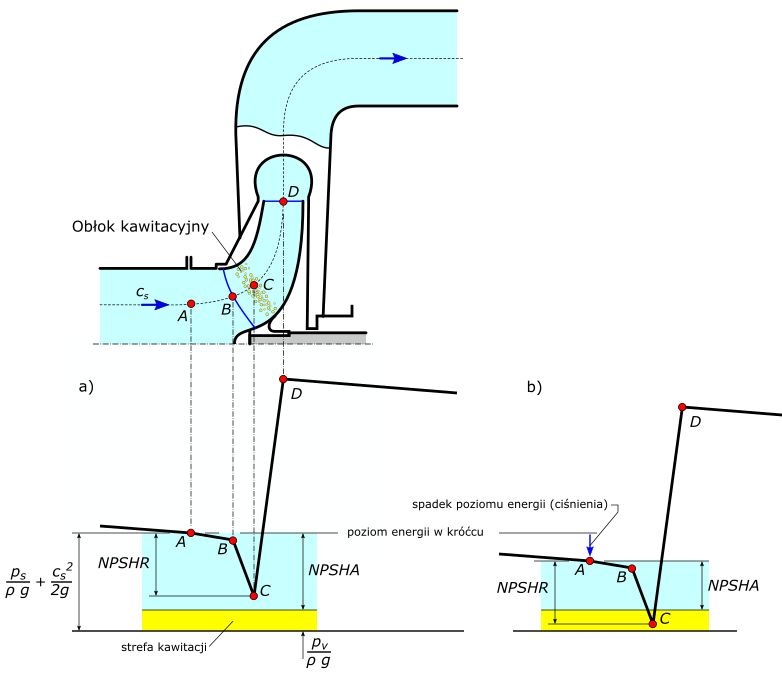
 Rys. 1. Przebieg linii energii w pompie i układzie pompowym, a – praca bezkawitacyjna, b – praca w strefie kawitacji
Rys. 1. Przebieg linii energii w pompie i układzie pompowym, a – praca bezkawitacyjna, b – praca w strefie kawitacji
Na podstawie badań H.B. Taylora i L.F. Moddy`ego Dieter Thoma [Troskolański A.T. Łazarkiewicz Sz., Pompy wirowe]– niemiecki inżynier hydraulik, w 1925r sformułował następującą tezę:
Wysokość depresji dynamicznej Δh określonej jako:
\Delta h = h_B - h_C (1)
jest proporcjonalna do H – wysokości podnoszenia dla pompy lub spadu dla turbiny, wzór 2 .
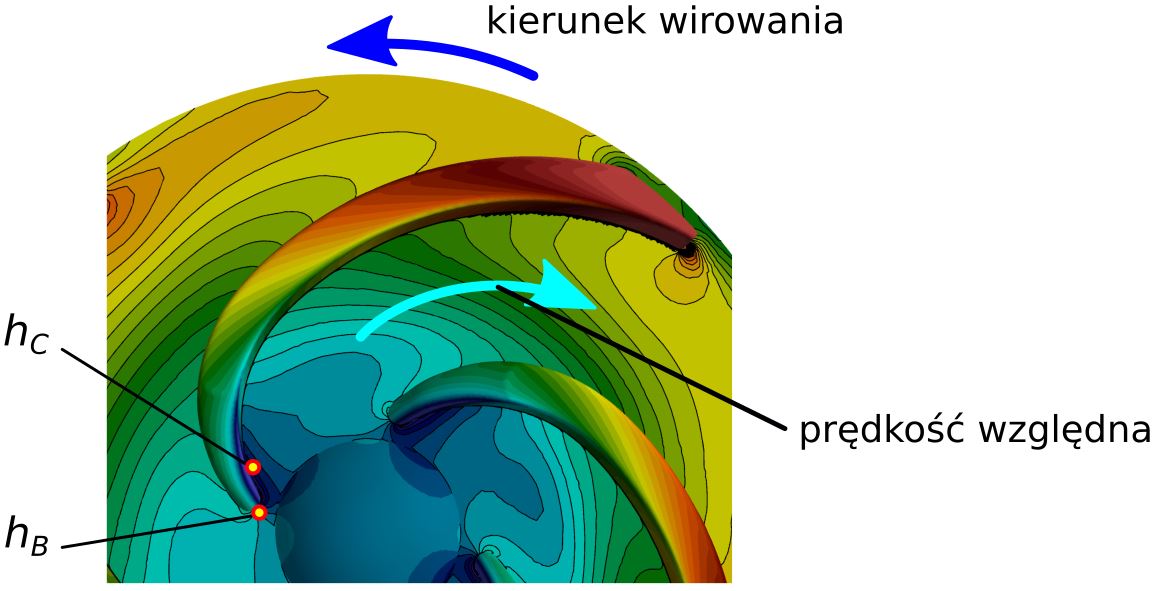 Rys. 2. Depresja dynamiczna na wlocie do wirnika maszyny przepływowej (turbina wodna, pompa)
Rys. 2. Depresja dynamiczna na wlocie do wirnika maszyny przepływowej (turbina wodna, pompa)
\Delta h = \sigma \cdot H (2)
σ - kawitacyjny wyróżnik D. Thomy (współczynnik Thomy) Δh - wysokość depresji dynamicznej H - wysokości podnoszenia pompy lub spad turbiny
Kawitacyjny współczynnik Thomy σ używany jest do oceny ryzyka wystąpienia kawitacji w pompach, turbinach i śrubach okrętowych.
Orientacyjne wartości współczynnika Thomy:
- Dla pomp odśrodkowych: σ ≈ 0.1 – 0.5
- Dla turbin wodnych: σ ≈ 0.2 – 0.4
- – Francisa: σ ≈ 0.1 – 0.4
- – Kaplana: σ ≈ 0.2 – 0.5
- – Peltona: σ ≈ < 0.1
- Dla śrub okrętowych: σ >1
Jeżeli przyjmiemy, że straty między króćcem ssawnym a krawędzią wlotową łopatki, punkty A i B, są niewielkie to możemy napisać:
NPSHR \approx \Delta h = \sigma \cdot H (3)
PAMIĘTAJ !
- Współczynnik kawitacyjny σ w przybliżeniu jest odpowiednikiem NPSH
- Wartość krytycznego współczynnika kawitacyjnego σkr podobnie jak NPSHR zależy od wielu parametrów konstrukcyjnych i eksploatacyjnych takich jak: geometria łopatek wirnika, prędkość obrotowa, liczba łopatek, punktu pracy itp.
Warto sprawdzić:
