Do budowy dynamicznych modeli matematycznych układów wykorzystujemy II zasadę dynamiki, która jest zapisywana w postaci równań ruchu.
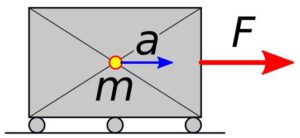
Rys.1. Przyśpieszenie liniowe
Dla ruchu postępowego:
m \cdot a = m \cdot {dv \over dt}= m \cdot {d^2x \over dt^2}= \Sigma F
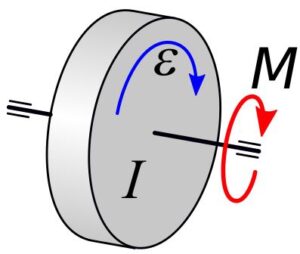
Rys.2. Przyśpieszenie kątowe
Dla ruchu obrotowego:
I \cdot \epsilon = I \cdot {{d \omega}\over dt}= I \cdot {d^2 \alpha \over dt^2}= \Sigma M
m – masa ciała [kg] I – moment bezwładności [kg*m2] x – przemieszczenie [m] α - kąt [rad] v - prędkość [m/s]ω - prędkość kątowa [m/s] a - przyśpieszenie liniowe [m/s2] ε - przyśpieszenie kątowe [rad/s2] t – czas [s], ∑F – suma sił [ N ] ∑M – suma momentów [Nm]
Warto sprawdzić:
