Pod wpływem ciśnienia wewnętrznego rurociąg się odkształca – zwiększa swoją średnicę.
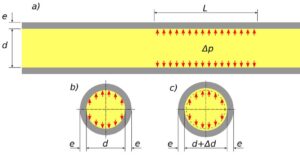
Rys.1. Odkształcenie rurociągu
Siłę parcia F w przekroju osiowym rurociągu wywołaną ciśnieniem opisuje wzór 1.
F = \Delta p \cdot d \cdot L (1)
Naprężenie w ściance rurociągu wywołane siła parcia F opisuje wzór 2.
\sigma = {F \over 2 \cdot e \cdot L} (2)
Przez podstawienie wzoru 1 do 2 otrzymamy wzór 3 na naprężenia w ściance rurociągu.
\sigma = {\Delta p \cdot d \cdot L \over 2 \cdot e \cdot L} = {\Delta p \cdot d \over 2 \cdot e} (3)
Odkształcenie w przypadku ścianki rury można opisać wzorem 4.
\epsilon = {\Delta l \over l} = {\pi \cdot (d + \Delta d) - \pi \cdot d \over \pi \cdot d } = {\Delta d \over d} (4)
Zgodnie z prawem Hooke’a wiemy, że odkształcenie jest proporcjonalne do naprężenia i odwrotnie-proporcjonalne do modułu sprężystości, wzór 5.
\epsilon = {\Delta d \over d} = {\sigma \over E} (5)
Po podstawieniu wzoru 3 do 5 otrzymamy wzór 6 na przyrost średnicy rurociągu na skutek wzrostu ciśnienia.
\Delta d = {d^2 \over 2 \cdot e \cdot E} \cdot \Delta p (6)
d – średnica rurociągu Δd – przyrost średnicy E – moduł sprężystości materiału rurociągu e – grubość ścianki rurociągu p – ciśnienie L - długość F - siła σ - naprężenia ε - odkształcenie
Przyrost objętości cieczy w rurociągu spowodowany przyrostem jego średnicy możemy opisać wzorem 7.
\Delta V = \pi \cdot d \cdot L \cdot {\Delta d \over 2} (7)
Po podstawieniu równania 6 do 7 otrzymamy równanie 8 na przyrost objętości rurociągu ΔV w zależności od przyrostu ciśnienia Δp.
\Delta V = {\pi \cdot d^3 \cdot L \over 4 \cdot e \cdot E} \cdot \Delta p (8)
Po uwzględnieniu, że przyrosty są małe w porównaniu do objętości rurociągu możemy równanie 8 przekształcić do postaci 9:
\Delta V = {\pi \cdot d^2 \cdot L \over 4} \cdot {d \over e \cdot E} \cdot \Delta p = V\cdot {d \over e \cdot E} \cdot \Delta p (9)
V - objętość cieczy
V – przyrost objętości rurociągu
Po podzieleniu obustronnie równania przez czas, ostatecznie natężenie przepływu, spowodowane przyrostem średnicy będzie opisywał wzór 10.
Q_r = {dV \over dt} = V \cdot {d \over e \cdot E} \cdot {dp \over dt} (10)
Uwaga: W obliczeniach pomijamy naprężenia osiowe
PAMIĘTAJ
- Rurociąg na rys. 1 nie jest utwierdzony, rurociąg swobodnie przemieszcza się wzdłuż osi
- We wzorze 4 pominięto wpływ naprężenia osiowego
Warto sprawdzić:
