Projekt wirnika odśrodkowego cz. 3 – kształtowanie wirnika

Kontynuacja obliczeń z cz.1 – obliczenia wstępne

Kontynuacja obliczeń z cz.2 – obliczenia części przepływowej

11. Obliczenia zarysu łopatki

11.1. Parametry wlotu i wylotu wirnika

r₁ = 0,04 – promień wlotowy
b₁ = 0,018 – szerokość wirnika na wlocie
β₁ = 0,320 = 18,35° – kąt łopatki na wlocie
β_1k = 0,419 = 24° – kąt konstrukcyjny łopatki na wlocie
c_m1 = 4,07 – prędkość merydionalna na wlocie
c_m1k = 5,46 – prędkość merydionalna na wlocie dla konta konstrukcyjnego
s₁ = 0,003 – grubość łopatki na wlocie
u₁= $12, 2 7 - prędkość unoszenia na wlocie$
φ₁ = $1, 25 9 - współczynnik przesłonięcie przekroju na wlocie$
r₂ = 0,1 – promień wylotowy
b₂ = 0,008 – szerokość wirnika na wylocie
β₂ = 0,576 = 33° – kąt łopatki na wylocie
s₂ = 0,004 – grubość łopatki na wylocie
φ₂ = $1, 089 - współczynnik przesłonięcie przekroju na wylocie$
Z = 7 – liczba łopatek
ω = $306, 8 - prędkość kątowa wirnika$

11.2. Założenia obliczeń szkieletowej łopatki

szkieletowa łopatki wyznaczona zostanie metodą punktową 2D
w obliczeniach uwzględniamy kąt natarcia
współrzędne biegunowe łopatki zostaną wyznaczone dla 10 punktów
sinus kąta łopatki sin β określa równanie

$sin \ \beta = {c_{mn} \over w} + {s \over t}$

sinus kąta konstrukcyjnego łopatki sin β_k zostanie obliczony z zależności

$sin \ \beta_k = {c_{mnk} \over w_k} + {s \over t}$ (1)

współrzędna kątowa zostanie obliczony z zależności

$\theta = \Sigma_{r_1}^r {1 \over r \cdot tg \ \beta_k} \cdot \Delta r$ (2)

11.3. Obliczenia prędkości konstrukcyjnych na wlocie i wylocie

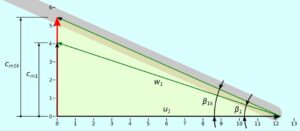
Rys. 1. Konstrukcyjny trójkąt prędkości na wlocie

Konstrukcyjna prędkość merydionalna na wlocie

$c_{m1k} = u_1 \cdot tg ( \beta_{1k}) = 12,27 \cdot tg(0,419) = 5,46$ (3)

Konstrukcyjna prędkość względna na wlocie

$w_{1k} = {u_1 \over cos ( \beta_{1k} ) } = {12,27 \over cos ( 0,419 )} = 13,43$ (4)

Prędkość merydionalna netto na wlocie (bez łopatek)

$c_{mn1} = {c_{m1} \over \varphi_1} = {4,07 \over 1,259} = 3,23$ (5)

Konstrukcyjna prędkość merydionalna netto na wlocie (bez łopatek)

$c_{mn1k} = {c_{m1k} \over \varphi_1} = {5,46 \over 1,259} = 4,34$ (6)

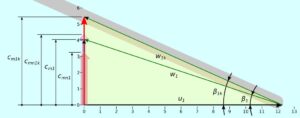
Rys. 2. Prędkości netto na wlocie

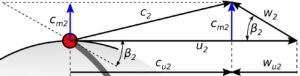
Rys. 3. Trójkąt prędkości na wylocie

Ponieważ, kąt natarcia łopatki nie zmienia kąta konstrukcyjnego na wylocie możemy przyjąć, że prędkości konstrukcyjne na wylocie są takie same jak prędkości obliczeniowe.

$c_{m2k} = c_{m2} = 3,12$ (7)

$c_{mn2k} = c_{mn2} = {c_{m2} \over \varphi_1} = {3,12 \over 1,089} = 2,86$ (8)

$w_{2k} = w_2 = {c_{m2} \over sin ( \beta_2 ) } = {3,12 \over sin ( 0,576 )} = 5,73$ (9)

11.4. Dane do obliczeń tabelarycznych

Liczba przedziałów n jest równa liczbie punktów pomniejszonych o 1.

$n = 10-1 = 9$ (10)

Zakładam stały przyrost promienia – krok całkowania

$\Delta r = {r_2 - r_1 \over n} = {0,1 - 0,04 \over 9} = 0,0067$ (11)

Zakładam liniową zmianę prędkości merydionalnej i względnej

$\Delta c_{mnk} = {c_{mn2k} - c_{mn1k} \over n} = {2,86 - 4,34 \over 9} = -0,164$ (12)

$\Delta w_k = {w_{2k} - w_{1k} \over n} = {5,73 - 13,43 \over 9} = -0,857$ (13)

Zakładam także stopniowe zwiększanie grubości łopatki w części wlotowej.

Dane do obliczeń są pokazane w tabeli 1 i na rys. 4.

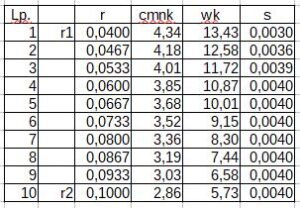
Tab. 1. Dane do obliczeń

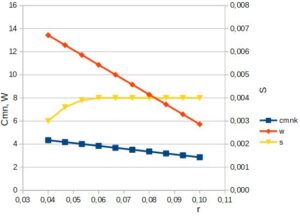
Rys. 4. Zmiana wartości: prędkości merydionalnej netto, prędkości względnej oraz grubości łopatki w zależności od promienia

11.5. Obliczenia współrzędnej kątowej łopatki

Podziałka t została obliczona ze wzoru opisanego w części 2.

Sinus kąta łopatki został obliczony ze wzoru 1, a współrzędna kątowa ze wzoru 2.

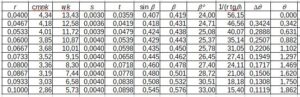
Tab. 2. Obliczenia kąta i współrzędnej kątowej szkieletowej łopatki

Zarys szkieletowej łopatki, średnicę wewnętrzną i średnicę zewnętrzną wirnika można narysować we współrzędnych kartezjańskich stosując proste przekształcenie.

$x = r \cdot cos ( \theta )$ (14)

$y = r \cdot sin ( \theta )$ (15)

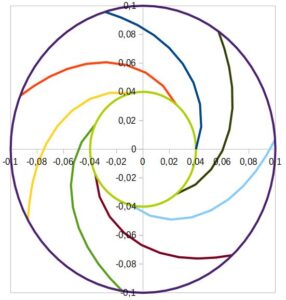Tab. 5. Szkieletowe łopatek wirnika

12. Obliczenia szerokości wirnika w przekroju merydionalnym

Do obliczeń szerokości wirnika wykorzystujemy wartości prędkości merydionalnej netto c_mn (bez uwzględnianie kata natarcia).

Zmiany prędkości merydionalne netto c_mn, są proporcjonalne do zmian konstrukcyjnej prędkości merydionalnej netto c_mnk, jak to pokazano na rys. 5.

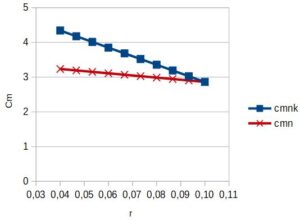
Rys. 5. Zmiana prędkości merydionalnej netto

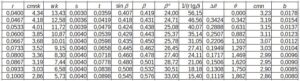
Tab. 3. Obliczenia szerokości wirnika

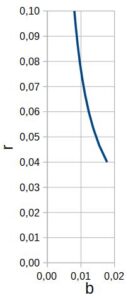
Rys. 6. Zmiana szerokości wirnika

13. Analiza przekroju przepływowego

Sprawdzenie kąta pokrycia δ.

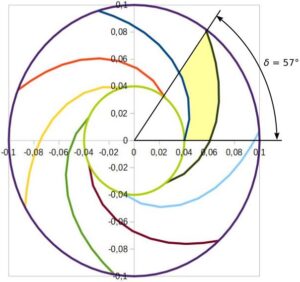
Rys. 7. Kąt pokrycia łopatki

Zalecane wg W. Jędrala – Pompy wirowe, kąty pokrycia powinny się mieścić w przedziale δ = 40° ÷ 60° w wyjątkowych przypadkach δ = 30° ÷ 80°.

Uzyskany w trakcie obliczeń kąt pokrycie łopatki mieści się w zalecanym przedziale.

Sprawdzenie przekroju przepływowego

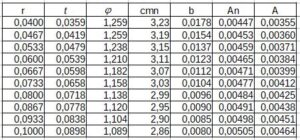
Tab. 4. Obliczenia pola przekroju przepływowego

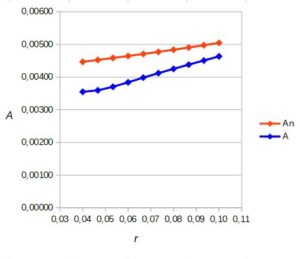Rys. 8. Pole przekroju przepływowego A i pole przekroju przepływowego netto A_n w zależności od promienia

W. Jędral – Pompy wirowe, zaleca aby kształt wykresu pola przekroju A_n nie miał punktów przegięcia.

Uzyskany w trakcie obliczeń kształt wykresu A_n jest prawidłowy.

Sprawdzenie przekroju przepływowego wzdłuż średniej linii prądu

Szerokość kanału wyznaczamy wykreślnie, patrz rys. 9, przez wpisanie między sąsiadujące łopatki okręgów o średnicy a.

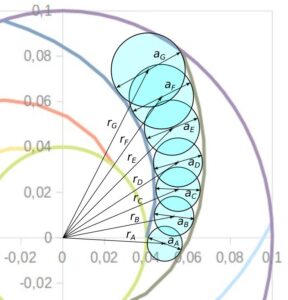
Rys. 9. Szerokość kanału przepływowego w przekroju prostopadłym

Szerokość kanału b dla wyznaczonych wykreślnie promieni, patrz rys. 9, odczytujemy z wykresu rys.6. Dobrym rozwiązaniem jest także sporządzenie wykresu b(r) i ewentualna jego aproksymacja krzywą wykładniczą.

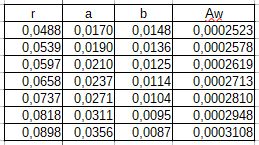
Tab. 5. Obliczenia pola przekroju przepływowego wzdłuż średniej linii prądu

Pole przekroju kanału wzdłuż średniej linii prądu A_w (prostopadle do prędkości w) wyznaczamy ze wzoru 16.

$A_w = a \cdot b$ (16)

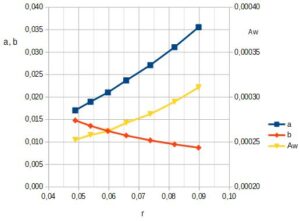
Rys. 10. Pola przekroju przepływowego wzdłuż średniej linii prądu

a – szerokość kanału w przekroju prostopadłym, b – szerokość kanału w przekroju merydionalnym, A_w – pole przekroju przepływowego

Z przeprowadzonej analizy wynika, że wzdłuż średniej linii prądu pole przekroju kanału przepływowego zmienia się monotonicznie, a krzywa zmian, w części środkowej, jest lekko wygięta do dołu.

Uzyskany w trakcie obliczeń kształt wykresu A_w jest prawidłowy.

PAMIĘTAJ !

To jest ćwiczenie dla studentów a nie „prawdziwy projekt”
Do obliczeń szkieletowej używamy prędkości konstrukcyjnych c_mnk i w_k
Do obliczeń szerokości wirnika używamy prędkości obliczeniowych c_mn
Uzyskane wyniki nie są dokładne, ze względu na stosowanie zaokrągleń, mimo to uzyskana dokładność jest wystarczająca dla stworzenia projektu bryłowego wirnika w programie CAD
Stworzony projekt bryłowy wirnika powinien być poddany analizie CFD

Warto sprawdzić: