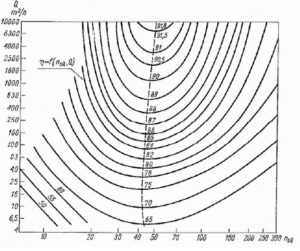
Rys.1. Wykres Gradewalda

Rys.2. Powierzchnia aproksymująca wykres Gradewalda
Równanie aproksymacyjne wykres Gradewalda:
\eta=a+b \cdot ln(n_q)+c \cdot ln^2(n_q)+d \cdot ln^3(n_q) +
+e \cdot ln(Q) + f \cdot ln^2(Q) + g \cdot ln^3(Q) + h \cdot ln^4(Q)
Gdzie:
- η – sprawność całkowita [%]
- Q – wydajność optymalna [m3/h]
- nq – wyróżnik szybkobieżności
- a = -69,49
- b = 83,025
- c = -16,1397
- d = 0,9177241
- e = -4,4161
- f = 4,42300
- g = -0,6969241
- h = 3,3428469
PAMIĘTAJ !
- Aproksymacja jest dokładna w centrum aproksymowanego obszaru
- Na końcach aproksymowanego obszaru a tym bardziej przy ekstrapolacji, wartości funkcji mogą znacząco odbiegać od wartości z wykresu
Warto sprawdzić:
- Wyróżnik szybkobieżności
- Oszacowanie sprawności całkowitej – Strachovsky
- Oszacowanie sprawności całkowitej – MEI
