Podstawy rachunku prawdopodobieństwa
Gotowość pompowni równoległych (układów złożonych) oblicza się na podstawie rachunku prawdopodobieństwa zdarzeń.
- Prawdopodobieństwo zdarzenia pewnego wynosi 1.
- Prawdopodobieństwo, że pompa jest gotowa do pracy, oznaczamy jako A.
- Prawdopodobieństwo, że pompa nie jest gotowa do pracy, określa wzór 1.
A' = 1 - A (1)
- Prawdopodobieństwo, że układ złożony z urządzeń zależnych jest gotowy do pracy, obliczamy ze wzoru 2.
A = A_1 \cdot A_2 (2)
- Prawdopodobieństwo, że układ złożony z urządzeń niezależnych jest gotowy do pracy, obliczamy ze wzoru 3.
A = A_1 + A_2 (3)
Przykłady obliczeń gotowości układów równoległych
Zasady obliczeń gotowości układów równoległych przedstawię na przykładach pompowni z: jedną, dwoma, trzema i czterema pompami.
Zakładam, że gotowość wszystkich pomp Ap w pompowniach jest jednakowa.
Ap = 0,9
n - liczba pomp w pompowni m - liczba pomp niezbędna do prawidłowej pracy pompowni r = (n-m) - liczba pomp rezerwowych Ap - gotowość pojedynczej pompy App(m+r) = App(m+(n-m)) - gotowość m pomp z n pomp w pompowni
Pompownia jedno-pompowa (1)
![]()
Rys. 1. Pompownia jedno-pompowa (1)
W pompowni jest jedna pompa, więc gotowość pompowni jest równa gotowości pojedyńczej pompy.
A_{pp(1)}=A_p=0,9 (4)
Pompownia dwu-pompowa (2)
Rys. 2. Pompownia dwu-pompowa (2)
W pompowni są dwie pompy. Aby pompownia działała prawidłowo konieczna jest praca obu pomp równocześnie. Gotowość pompowni obliczamy na podstawie wzoru 2.
A_{pp(2)} = A_p^2 = 0,9^2 = 0,81 (5)
Pompownia dwu-pompowa z pompą rezerwową (1+1)
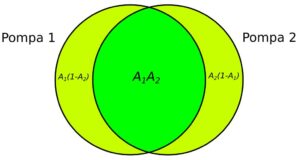
Rys. 3. Pompownia dwu-pompowa (1+1)
W pompowni są dwie pompy. Aby pompownia działała prawidłowo konieczna jest praca jednej z pomp. Gotowość pompowni to suma prawdopodobieństwa, że: obie pompy są sprawne, pierwsza pompa jest sprawna a druga nie i druga jest sprawna a pierwsza nie, wzory 2 i 3.
A_{pp(1+1)} = A_p \cdot A_p + 2 \cdot A_p \cdot (1-A_p) = (6)
0,9 \cdot 0,9 + 2 \cdot 0,9 \cdot (1-0,9)= 0,81+2 \cdot 0,09 = 0,99
Pompownia trój-pompowa (3)
Rys. 4. Pompownia trój-pompowa (3)
W pompowni są trzy pompy. Aby pompownia działała prawidłowo, konieczna jest praca wszystkich pomp równocześnie. Gotowość pompowni obliczamy na podstawie wzoru 2.
A_{pp(3)} = A_p^3 = 0,9^3 = 0,729 (7)
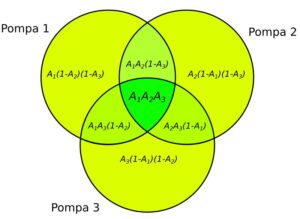
Pompownia trój-pompowa z jedną pompą rezerwową (2+1)
Rys. 5. Pompownia trój-pompowa (2+1)
W pompowni są trzy pompy. Aby pompownia działała prawidłowo, konieczna jest praca dwóch pomp. Gotowość pompowni to suma prawdopodobieństwa, że: wszystkie pompy są sprawne i sprawna jest dowolna para pomp. Do obliczeń wykorzystujemy wzory 2 i 3.
A_{pp(2+1)} = A_p^3 + 3 \cdot A_p^2 \cdot (1-A_p) (8)
= 0,9^3 + 3 \cdot 0,9^2 \cdot (1-0,9) = 0,729 + 3 \cdot 0,81 \cdot 0,1 = 0,972
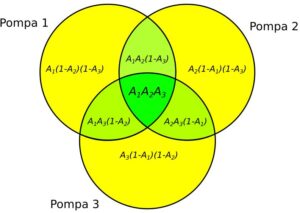
Pompownia trój-pompowa z dwoma pompami rezerwowymi (1+2)
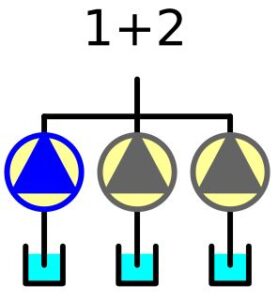
Rys. 6. Pompownia trój-pompowa (1+2)
W pompowni są trzy pompy. Aby pompownia działała prawidłowo, konieczna jest praca jednej z pomp. Gotowość pompowni to suma prawdopodobieństwa, że: wszystkie pompy są sprawne, sprawna jest dowolna para pomp oraz sprawna jest tylko jedna dowolna pompa. Porównaj rysunki 5 i 6. Do obliczeń wykorzystujemy wzory 2 i 3.
A_{pp(1+2)} = A_p^3 + 3 \cdot A_p^2 \cdot (1-A_p) + 3 \cdot A_p \cdot (1-A_p)^2 (9)
= 0,9^3 + 3 \cdot 0,9^2 \cdot (1-0,9) + 3 \cdot 0,9 \cdot (1-0,9)^2 =
0,729 + 3 \cdot 0,081 + 3 \cdot 0,009 = 0,999
Ogólny wzór na obliczanie gotowości układu równoległego pomp [Florjancic D.]
Zauważ, że we wzorach 6, 7 i 8 dodawane są kolejne człony, opisujące prawdopodobieństwo wystąpienia kolejnych zdarzeń. Na tej podstawie można sformułować ogólny wzór na gotowość dowolnej pompowni, przy założeniu, że gotowość pomp jest jednakowa.
A_{m+r}=\sum_{i=m}^{n} \left [ {n \choose i} \cdot A^i \cdot (1-A)^{n-i} \right] (10)
Współczynnik Newtona określony jest wzorem 11.
{n \choose i} = {n! \over i! \cdot (n-i)!} (11)
n - liczba pomp w pompowni m - liczba pomp niezbędna do prawidłowej pracy pompowni r = (n-m) - liczba pomp rezerwowych A - gotowość pojedynczej pompy Am+r = Am+(n-m) - gotowość m pomp z n pomp w pompowni
Gotowość dla dowolnej konfiguracji pompowni może być obliczona w arkuszu kalkulacyjnym, załączonym na końcu strony.
Pompownia cztero-pompowa (4)
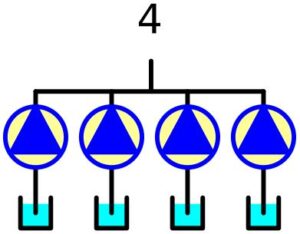
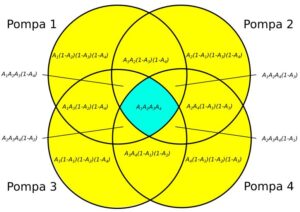
Rys. 7. Pompownia cztero-pompowa (4)
A_{pp(4)} = A_p^4 = 0,9^4 = 0,6561
Pompownia cztero-pompowa z jedną pompą rezerwową (3+1)
Rys. 8. Pompownia cztero-pompowa (3+1)
A_{pp(3+1)} = 0,9477
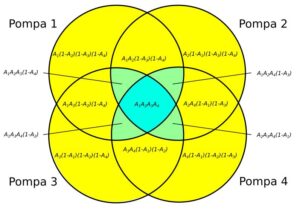
Pompownia cztero-pompowa z dwoma pompami rezerwowymi (2+2)
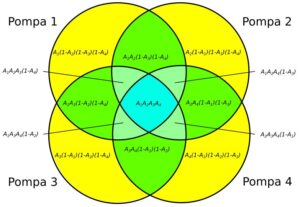
Rys. 8. Pompownia cztero-pompowa (2+2)
A_{pp(2+2)} = 0,9963
Pompownia cztero-pompowa z trzema pompami rezerwowymi (1+3)
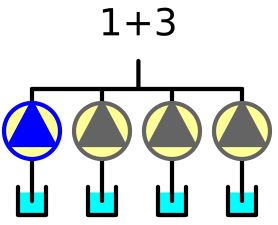
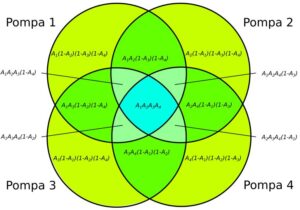
Rys. 9. Pompownia cztero-pompowa (1+3)
A_{pp(1+3)} = 0,9999
Porównanie niezawodności pompowni równoległych
Średni czas między niesprawnościami pompowni MTBFpp można wyznaczyć ze wzoru 12.
MTBF_{pp} = {MTTR \over 1 - MTBF_p} (12)
W tabeli 1 zebrano wartości gotowości i czasów MTBF pompowni z: jedną, dwoma, trzema i czterema pompami.
Tab. 1. Wpływ liczby pomp rezerwowych na MTBF układu, przy średnim czasie naprawy MTTR = 50 godzin
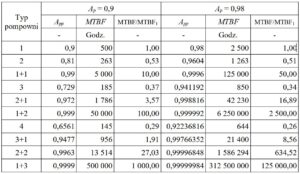
Z danych zestawionych w tabeli wynika, że dla Ap = 0,9:
- dodanie jednej pompy rezerwowej zwiększa MTBF 10 razy
- dodanie dwóch pomp rezerwowych zwiększa MTBF 100 razy
- dodanie trzech pomp rezerwowych zwiększa MTBF 1000 razy
Arkusze kalkulacyjne:
PAMIĘTAJ
- Nie sugeruj się gotowością pompy Ap = 0,9 lub 0,98. To tylko przykłady obliczeniowe
- Przytoczone przykłady można odnieść do: pomp, pompowni, w których pompy muszą współpracować równolegle, a nawet do całych systemów pompowych, wymagających współpracy równoległej układów pompowych.
- Im wyższa gotowości pomp i urządzeń, tym wyższa gotowość pompowni
- Im więcej pomp rezerwowych, tym MTBF jest większe
Warto sprawdzić:




