Charakterystyki rozruchowe pompy

Parametry energetyczne pompy wirowej na wyjściu (po stronie hydraulicznej) są opisane za pomocą charakterystyki przepływu H = f(Q), natomiast parametry na wejściu (od strony wału napędowego) są opisane za pomocą charakterystyki mocy P = f(Q) lub momentu na wale M = f(Q), przy określonej nominalnej prędkości kątowej ωn.

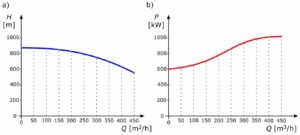
Rys. 1. Charakterystyki pompy wirowej: a) – charakterystyka przepływu, b) – charakterystyka mocy

Informacja źródłowa o przebiegu tych krzywych, odnoszących się do rzeczywiście produkowanych pomp, zapisana jest zwykle w postaci tabelarycznej:

Tab.1. Przykład punktów tworzących charakterystyki energetyczne pompy (n=2960 obr/min, ρ=1000 kg/m3)

\begin{matrix} Q & H & P \\{m^3}/h & m & kW \\0 & 875 & 602\\50 & 872 & 616\\100 & 861 & 644\\150 & 847 & 693\\200 & 823 & 770\\250 & 788 & 854\\300 & 742 & 924\\350 & 690 & 973\\400 & 630 & 1008 \\450 & 553 & 1015 \end{matrix}

Wartości pośrednie funkcji uzyskuje się przez aproksymację liniową lub krzywoliniową między punktami.

Charakterystyki pracy pompy, przy prędkościach kątowych różnych od nominalnej, z wystarczającą do obliczeń dynamicznych dokładnością można wyznaczyć, z pominięciem zmian sprawności, na podstawie praw podobieństwa maszyn wirowych.

Przeliczenia krzywych dokonujemy przez przeliczenie wartości punktów, tabeli źródłowej np. tab. 1.

Q=Q_n \cdot {\omega \over \omega_n}

H=H_n \cdot ({\omega \over \omega_n})^2

P=P_n \cdot ({\omega \over \omega_n})^3

M=M_n \cdot ({\omega \over \omega_n})^2

ω - prędkość kątowa,
Q - wydajność,
H - wysokość podnoszenia,
P - moc na wale,
M - moment na wale,
n - indeks dolny, wartość nominalna,
- - bez indeksu, wartość bieżąca.

W wielu przypadkach, podczas modelowania dynamicznego łatwiejszym sposobem jest przeliczanie sygnału wejściowego (Q, n) i wyjściowego (H, P, M) zamiast przeliczania położenia punktów.

Pojęcia "sygnał" będę używali do opisu wielkości zmieniających się w czasie.

Dla wysokości podnoszenia całą operację możemy zapisać wzorem:

H=H_n(Q{\omega_n \over \omega}) \cdot ({\omega \over \omega_n})^2

H - wysokość podnoszenia dla aktualnej prędkości kątowej
Q - przepływ dla aktualnej prędkości kątowej
Hn(Q) - charakterystyka przepływu dla nominalnej prędkości kątowej
ω - aktualna prędkość kątowa
ωn - nominalna prędkość kątowa

Teoretycznie, zgodnie z prawem podobieństwa maszyn wirowych, punkty charakterystyki momentu obciążenia pompy przemieszczają się po parabolach 2-go stopnia o wierzchołku w początku układu współrzędnych – rys. 2b (linia przerywana).

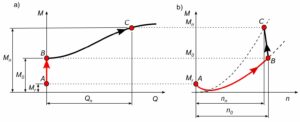
Rys.2. Moment pompy wirowej (charakterystyka mechaniczna) podczas rozruchu, a) w funkcji wydajności, b) w funkcji prędkości obrotowej

W rzeczywistości, w czasie rozruchu, dla małych prędkości obrotowych krzywa ta odbiega od kształtu parabolicznego. Jak pokazano na rys. 2b (linia czerwona), dla małych prędkości obrotowych, rzeczywisty moment obciążenia jest wyższy od teoretycznego. Jest to spowodowane występowaniem tarcia spoczynkowego w łożyskach i uszczelnieniach pompy. Ponadto, szczególnie w małych pompach, na tarcie ma duży wpływ sedymentacja zanieczyszczeń wewnątrz pompy.

Po rozpoczęciu wirowania, opory tarcia maleją, gdyż: współczynnik tarcia ruchowego jest znacznie mniejszy od współczynnika tarcia spoczynkowego oraz niszczone są struktury powstałe podczas sedymentacji. Ponadto, wskutek wydzielającego się ciepła, rośnie temperatura i spada lepkość smaru w łożyskach, co z kolei powoduje dalszy spadek oporów ruchu pompy.

Rzeczywistą charakterystykę momentu rozruchowego określana producent pompy.

Przy braku charakterystyki „fabrycznej”, do wyznaczenia zmian momentu rozruchowego można wykorzystać teorię podobieństwa uzupełnioną o  kwadratowy model strat mechanicznych dla małych prędkości obrotowych (od zera do ok. 30% nominalnej prędkości obrotowej).

Wartość momentu rozruchowego Mr pompy (dla zerowej prędkości obrotowej),   stanowi zwykle 10 do 20% momentu nominalnego Mn.

Paraboliczny model strat mechanicznych w czasie rozruch, dla prędkości względnych ω/ωn od 0 do 0,3, opisuje równanie:

M_m=(0,1 \div 0,2) \cdot M_n \cdot (1 - {\omega \over \omega_n}{1 \over 0,3})^2

Ostatecznie, przybliżony wzór na moment pompy w czasie rozruchu ma postać:

M=M_n(Q{\omega_n \over \omega}) \cdot ({\omega \over \omega_n})^2+M_m

M - moment
Mn - moment nominalny
Mn(Q) - charakterystyka momentu  
Mm - moment strat mechanicznych
Q - przepływ dla aktualnej prędkości kątowej
ω - aktualna prędkość kątowa
ωn - nominalna prędkość kątowa

 

PAMIĘTAJ !

  • Wydajność pompy i wysokość podnoszenia pompy można, z dużą dokładnością w dużym zakresie, przeliczać na inne prędkości obrotowe, na podstawie teorii podobieństwa
  • Moment rozruchowy pompy Mr, dla zerowej prędkości obrotowej, nie jest równy ZERO
  • Charakterystyka momentu rozruchowego pompy powinna być udostępniona przez jej producenta.

 

Warto sprawdzić: