Do magazynowania energii hydraulicznej w układach pompowych, stosowane są akumulatory gazowe – akumulatory hydrauliczne.
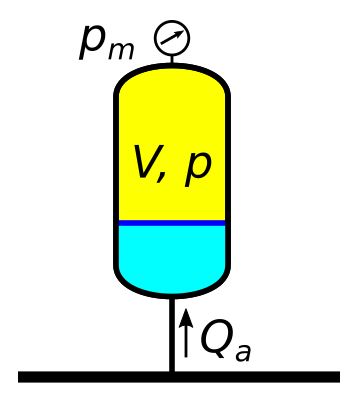
Rys. 1. Schemat ideowy akumulatora gazowego
Akumulator gazowy zbudowany jest ze zbiornika w którego górnej części znajduje się gaz. Gaz pełni w nim rolę sprężyny. Przy wzroście ciśnienia w układzie gaz jest sprężany, a ciecz wpływa do dolnej części zbiornika. Akumulatory gazowe są także nazywane: akumulatorami hydraulicznymi, powietrznikami, hydroforami, naczyniami wyrównawczymi itp.
Ciśnienie i objętość gazu w akumulatorze gazowym wiąże równanie politropy 1.
p \cdot V^n = p_0 \cdot V_0^n = const (1)
p0 - absolutne ciśnienie początkowe [ Pa ], p - ciśnienie absolutne [ Pa ], V0 -objętość początkowa gazu [ m3 ], V - objętość gazu[ m3 ], n - wykładnik politropy.
Ciśnienie absolutne opisuje wzór 2.
p = p_m + p_b (2)
p - ciśnienie absolutne [ Pa ], pm - ciśnienie manometryczne, wskazanie manometru [ Pa ], pb - ciśnienie barometryczne [ Pa ].
Natężenie przepływu cieczy do akumulatora możemy zapisać wzorem 3.
Q_a = -{dV \over dt} = - {dV \over dp}\cdot{dp \over dt} (3)
Ponieważ zmniejszenie objętości gazu powoduje napływ cieczy do akumulatora, pochodna objętości po czasie ma przeciwny znak niż natężenie przepływu akumulatora. Pochodną objętości po ciśnieniu możemy obliczyć z równania politropy 4.
V =V_0 \cdot p_0^{1 \over n} \cdot p^{-{1 \over n}} (4)
Po obliczeniu pochodnej względem ciśnienia dla lewej i prawej strony otrzymamy wzór na zmianę objętości od ciśnienia w postaci 5.
{dV \over dp} = - {V_0 \over n} \cdot p_0^{1 \over n} \cdot p^{-{\left ( {1 \over n} + 1 \right )}} (5)
Ostatecznie, podstawiając wyrażenie 5 do 3 otrzymamy wzór na natężenie przepływu do akumulatora w postać 6.
Q_A= {dV \over dt} = {V_0 \over n} \cdot p_0^{1 \over n} \cdot p^{-{\left( {1 \over n} + 1 \right) }} \cdot {dp \over dt} (6)
Dla wolno-zmiennych przebiegów ładowania akumulatora, dla których ciepło wytwarzane podczas sprężania gazu jest odprowadzane na zewnątrz, można przyjąć izotermiczny przebieg przemiany. W tym przypadku wykładnik politropy przyjmuje wartość n=1. Zmianę ciśnienia i objętość gazu w akumulatorze w tym przypadku wiąże prawo Boyle’a i Mariotte’a 7.
p \cdot V = p_0 \cdot V_0 = const (7)
W tym przypadku, wzór na przepływ do akumulatora redukuje się do postaci 8.
Q_A= {dV \over dt} = {V_0 \cdot p_0 \over p^2} \cdot {dp \over dt} (8)
Dla przebiegów szybkozmiennych i akumulatorów izolowanych wymiana ciepła będzie utrudniona, a zatem można przyjąć adiabatyczny przebieg przemiany. W tym przypadku dla gazów dwuatomowych wykładnik politropy będzie miał wartość n = = 1,4.
W rzeczywistych warunkach proces ładowania akumulatora będzie się odbywał politropowo przy wykładniku politropy n = 1.0 do 1.4.
Popularną odmianą akumulatorów gazowych są akumulatory z przeponą, pokazane na rysunkach 2 i 3.
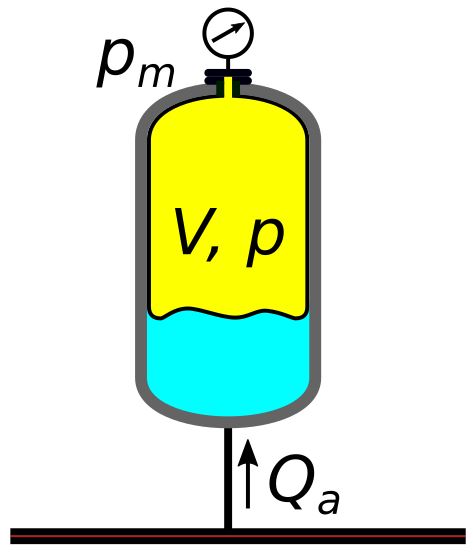
Rys.2. Schemat ideowy akumulatora przeponowego
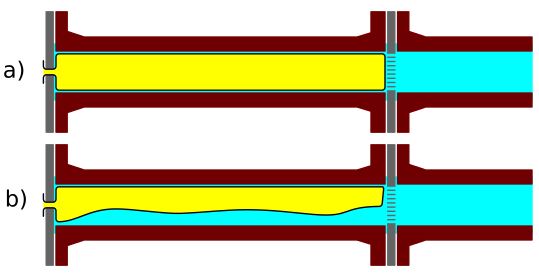
Rys. 3. Schemat akumulatora przeponowego w rurociągu a) p<p0, b) p>p0
Na rysunku 4 pokazano zmianę ciśnienia w akumulatorze w zależności od stopnia napełnienia, przy różnych ciśnieniach wstępnych. W przykładzie przyjęto, że objętość początkowa akumulatora wynosiła: V0 = 0.1 m3 (100 L), a ciśnienie wstępne wynosiło: p0 = 0, 2, 4, 6 bar.
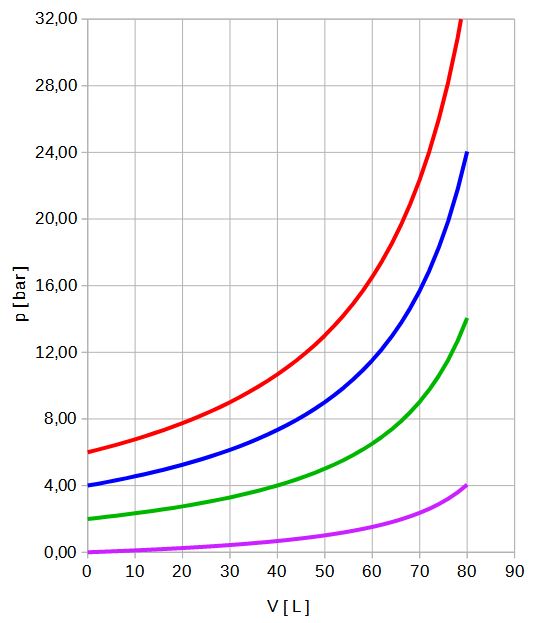
Rys.4. Zmiana ciśnienia w akumulatorze w zależności od objętości cieczy
PAMIĘTAJ !
- W akumulatorze gazowym można magazynować energię
- Ilość zmagazynowanej energii to: E=p \cdot V
- Akumulator gazowy można wykorzystać do zmniejszenia wahań ciśnienia w układzie – hydrofor
- Akumulatorem gazowym można zabezpieczyć rurociąg przed uderzeniem hydraulicznym
- Akumulator gazowy można wykorzystać do zmniejszenia pulsacji przepływy za pompą wyporową – powietrznik na ssaniu i tłoczeniu
Warto sprawdzić
