DRUGIE PRAWO KIRCHHOFFA
(Reguła pierścieni)
Drugie prawo Kirchhoffa (reguła pierścieni) stanowi, że w pierścieniu, algebraiczna suma różnic wysokości ciśnienia, na końcach przewodów (gałęzi), jest równa zeru.
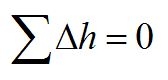
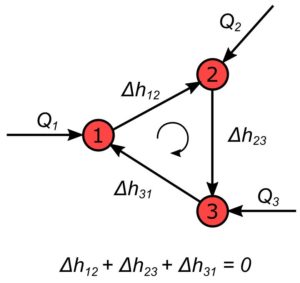
Regułę pierścieni można wyjaśnić na przykładzie pojedynczego oczka z trzema węzłami.
Konwencja zapisy zakłada, że dopływ do węzła jest dodatni i spadki ciśnienia liczone są w jedną stronę (w przykładzie zgodnie z kierunkiem obrotu wskazówek zegara)
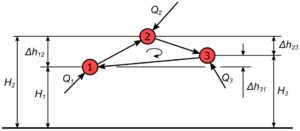
Q1 - dopływ do węzła 1 Q2 - dopływ do węzła 2 Q3 - dopływ do węzła 3 H1 - wysokość ciśnienia w węźle 1 H2 - wysokość ciśnienia w węźle 2 H3 - wysokość ciśnienia w węźle 4 Δh12 = H1-H2 - różnica wysokości ciśnienia między węzłami 1 i 2 Δh23 = H2-H3 - różnica wysokości ciśnienia między węzłami 2 i 3 Δh31 = H3-H1 - różnica wysokości ciśnienia między węzłami 3 i 1
PAMIĘTAJ !
- W węźle (w punkcie) może być tylko jedno ciśnienie, równe dla wszystkich końców podłączonych gałęzi
- Przynajmniej jeden z dopływów musi mieć inny znak niż pozostałe (Pierwsze prawo Kirchhoffa)
- Przynajmniej jeden ze spadków ciśnienia Δhij musi mieć inny znak niż pozostałe (w prezentowanym przykładzie: Δh12<0, Δh23>0, Δh31>0)
WARTO SPRAWDZIĆ:
