Wysokość podnoszenia pomp wirowych jest proporcjonalna do drugiej potęgi prędkości obrotowej.
H \sim n^2 \cdot d^2
{H_1 \over H_2} = ({n_1 \over n_2})^2
H_2 = H_1 \cdot ({n_2 \over n_1})^2
Q - wydajność H - wysokość podnoszenia n - prędkość obrotowa d - średnica wirnika
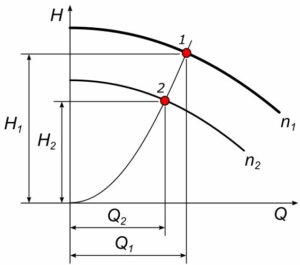
Rys.1. Przeliczanie wysokości H pomp wirowej zgodnie z wzorami podobieństwa
Przykład 1
n_1=2850, n_2=950, ({n_2 \over n_1})^2=({950 \over 2850})^2=({1 \over 3})^2={1 \over 9}
H_1 = 9, H_2=9 \cdot ({950 \over 2850})^2=9 \cdot {1 \over 9} = 1
Przykład 2
n_1=2900, n_2=1450, ({n_2 \over n_1})^2=({1450 \over 2900})^2=({1 \over 2})^2={1 \over 4}
H_1 = 4, H_2=4 \cdot ({1450 \over 2900})^2=4 \cdot {1 \over 4} = 1
Przykład 3
n_1=950, n_2=2850, ({n_2 \over n_1})^2=({2850 \over 950})^2=3^2=9
H_1 = 1, H_2=1 \cdot ({2850 \over 950})^2=1 \cdot 3^2 = 9
Przykład 4
n_1=1450, n_2=2900, ({n_2 \over n_1})^2=({2900 \over 1450})^2=2^2=4
H_1 = 1, H_2=1 \cdot ({2900 \over 1450})^2=1 \cdot 2^2 = 4
PAMIĘTAJ !
- Wysokość podnoszenia jest proporcjonalny do kwadratu prędkości obrotowej
Warto sprawdzić:
- Podstawowe wzory podobieństwa maszyn przepływowych
- Przelicz Q pompy wirowej na inną prędkości obrotową
- Przelicz P pompy wirowej na inną prędkości obrotową
