PODSTAWOWE RÓWNANIE MASZYN PRZEPŁYWOWYCH – RÓWNANIE EULERA
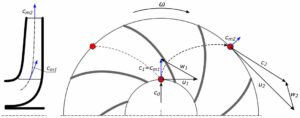
Rys. 1. Przepływ przez wirnik pompy odśrodkowej
Prędkość cząsteczki cieczy na wlocie i wylocie z wirnika możemy przedstawić w postaci trójkątów prędkości.
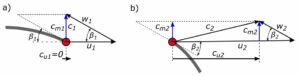
Rys. 2. Trójkąty prędkości
a) na wlocie przy dopływie prostopadłym, b) na wylocie z wirnika.
c - prędkość bezwzględna w - prędkość względna, równoległa do łopatki u - prędkość obwodowa cu - rzut prędkości na kierunek prędkości unoszenia 1 - indeks oznaczający wlot do wirnika 2 - indeks oznaczający wylot z wirnika
Kręt masy cieczy, przepływającej przez wirnik, można zapisać jako iloczyn: masy, składowej obwodowej prędkości i promienia.
K=m \cdot c_u \cdot r
K - kręt masy cieczy przepływającej przez wirnik m - masa cieczy przepływającej przez wirnik cu - rzut prędkości cieczy na kierunek unoszenia r - promień
Pochodna krętu K po czasie określa moment na wirniku.
M={dK \over dt}={{d ( m \cdot c_u \cdot r)} \over dt}
Po przejściu na różnice skończone przyrost krętu, między wlotem a wylotem z wirnika, możemy napisać jako:
M={{{\Delta m} \over {\Delta t}} \cdot {(c_{u2} \cdot r_2 - c_{u1} \cdot r_1)}}
Uwzględniając fakt, że masa cieczy, przepływająca przez pompę, określona jest wzorem:
m=V \cdot \rho
możemy napisać:
M={{\Delta V \cdot \rho} \over \Delta t} \cdot (c_{u2} \cdot r_2 - c_{u1} \cdot r_1) = {Q \cdot \rho} \cdot (c_{u2} \cdot r_2 - c_{u1} \cdot r_1)
Po pomnożeniu obu stron równania przez prędkość kątową, otrzymamy wzór na wewnętrzną moc hydrauliczną pompy w postaci:
P=M \cdot \omega={Q \cdot \rho} \cdot (c_{u2} \cdot u_2 - c_{u1} \cdot u_1)
P - wewnętrzna moc hydrauliczna, moc przekazywana przez łopatki M - moment na łopatkach wirnika Q - przepływ przez wirnik ρ - gęstość cieczy cu2 - składowa obwodowa prędkość na wylocie cu1 - składowa obwodowa prędkość na wlocie r2 - promień na wylocie z wirnika r1 - promień na wlocie do wirnika ω - prędkość kątowa r1ω=u1- prędkość obwodowa na wlocie r2ω=u2- prędkość obwodowa na wylocie
Po podstawieniu wzoru na moc hydrauliczną można napisać wzór na wysokość podnoszenia pompy jako:
P=Q \cdot H \cdot \rho \cdot g={Q \cdot \rho} \cdot (c_{u2} \cdot u_2 - c_{u1} \cdot u_1)
Ostatecznie po wyeliminowaniu Q i ρ otrzymamy:
H={1 \over g} \cdot (c_{u2} \cdot u_2 - c_{u1} \cdot u_1)
Zależność ta jest nazywana wzorem Eulera.